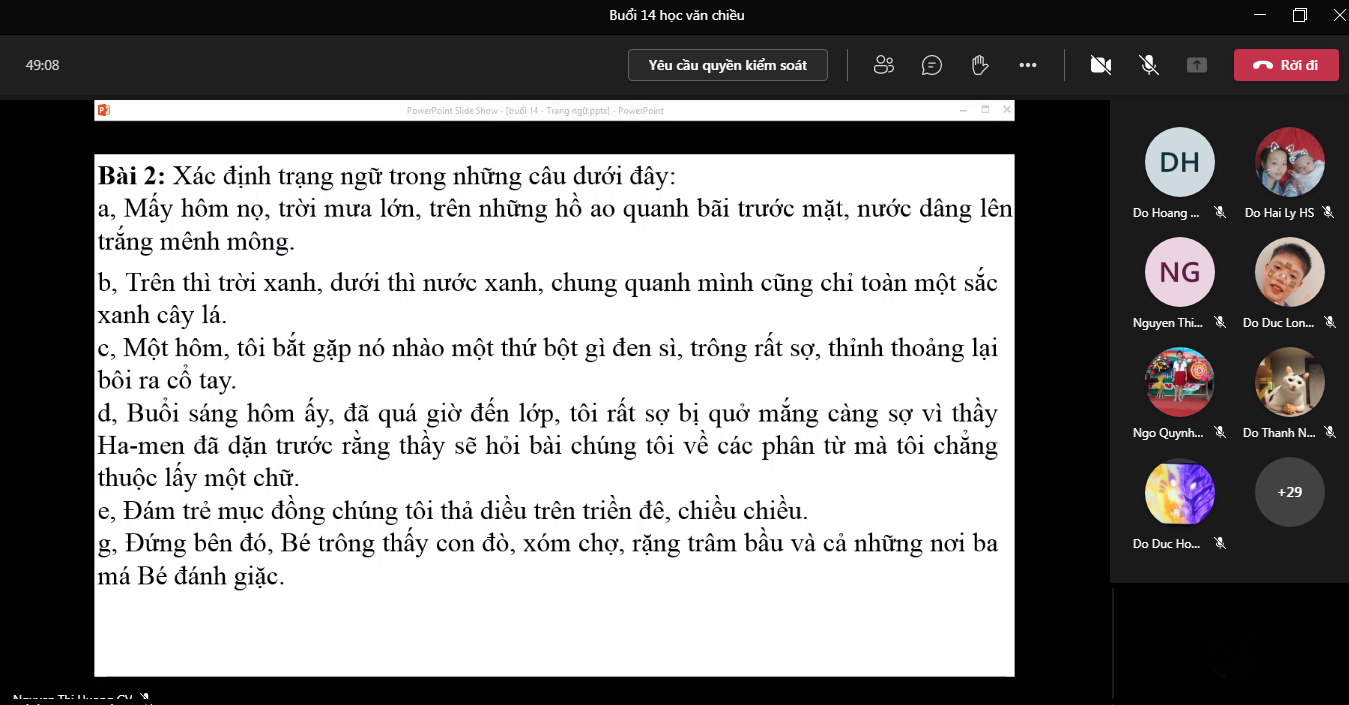
giúp em câu d , e , g với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
giúp em gọi tên thây thế của các ankan câu c e g với ạ
0
VT
1
22 tháng 10 2021
c: \(2x^3-50x=0\)
\(\Leftrightarrow2x\left(x-5\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
TN
2
AH
Akai Haruma
Giáo viên
13 tháng 9 2021
Lời giải:
d.
Áp dụng định lý Menelaus cho tam giác $BDF$ có $A,O,M$ lần lượt thuộc $BD, DF, BF$ và $A,O,M$ thẳng hàng:
$\frac{MF}{MB}.\frac{OD}{OF}.\frac{AB}{AD}=1$
$\Leftrightarrow \frac{MF}{MB}.1.2=1$
$\Leftrightarrow \frac{MF}{MB}=\frac{1}{2}$
$\Rightarrow \frac{BF}{MB}=\frac{3}{2}$
$\Leftrightarrow \frac{BC}{2MB}=\frac{3}{2}$
$\Leftrightarrow BC=3MB$ (đpcm)
TM
0
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
5 tháng 2 2022
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
HQ
0
d) Trạng ngữ : Buổi sáng hôm ấy , đã quá giờ đến lớp
e) Trên triền đê , chiều chiều
g) Đứng bên đó
d) Buổi sáng hôm ấy, đã quá giờ đến lớp
e) Đám trẻ mục đồng chúng tôi
g) Đứng bên đó