Cho đoạn mạch như phương trình : (R2//R3)ntR1 R1 = R2 = 10Ω , R3=12 Ω .Biết : Hiệu điện thế đoạn mạch là 24V . Tính điện trở tương đương của đoạn mạch? Tính cường độ dòng điện đi qua mỗi điện trở và hiệu điện thế giữa hai đầu mỗi điện trở.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
15 tháng 10 2021
Điện trở: \(R=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=16+\left(\dfrac{24.12}{24+12}\right)=24\Omega\)
Cường độ dòng điện R, R1 và R23:
\(\left\{{}\begin{matrix}I=U:R=24:24=1A\\I=I1=I23=1A\left(R1ntR23\right)\end{matrix}\right.\)
Hiệu điện thế R1 VÀ R23:
\(\left\{{}\begin{matrix}U1=R1.I1=16.1=16V\\U23=U-U1=24-16=8V\end{matrix}\right.\)
\(\Rightarrow U23=U2=U3=8V\)(R1//R23)
\(\left\{{}\begin{matrix}I2=U2:R2=8:24=\dfrac{1}{3}A\\I3=U3:R3=8:12=\dfrac{2}{3}A\end{matrix}\right.\)
7 tháng 10 2021
\(\Rightarrow\left\{{}\begin{matrix}a,R1//\left(R2ntR3\right)\Rightarrow Rtd=\dfrac{R1\left(R2+R3\right)}{R1+R2+R3}=6\Omega\\b,\Rightarrow\left\{{}\begin{matrix}U=U1=U23=24V\Rightarrow I1=\dfrac{U1}{R1}=\dfrac{8}{3}A\\I2=I3=\dfrac{U23}{R2+R3}=\dfrac{4}{3}A\\U2=I2.R2=8V\\U3=U-U2=16V\end{matrix}\right.\\c,R1//\left(R2ntRx\right)\Rightarrow Im=1,5.\dfrac{24}{6}=6A\\\Rightarrow Rtd=\dfrac{R1\left(R2+Rx\right)}{R1+R2+Rx}=\dfrac{9\left(6+Rx\right)}{15+Rx}=\dfrac{24}{Im}=4\left(\Omega\right)\Rightarrow Rx=1,2\Omega\end{matrix}\right.\)
VT
14 tháng 5 2019
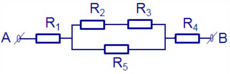
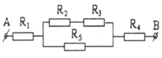
Phân tích đoạn mạch: R 1 nt (( R 2 n t R 3 ) // R 5 ) nt R 4 .
R 23 = R 2 + R 3 = 10 Ω ; R 235 = R 23 R 5 R 23 + R 5 = 5 Ω
R = R 1 + R 235 + R 4 = 12 Ω ; I = I 1 = I 235 = I 4 = U A B R = 2 A
U 235 = U 23 = U 5 = I 235 . R 235 = 10 V
I 5 = U 5 R 2 = 1 A ; I 23 = I 2 = I 3 = U 23 R 23 = 1 A
N
21 tháng 10 2021
a. \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(80+40\right)60}{80+40+60}=40\Omega\)
b. \(U=U12=U3=IR=40.0,15=6V\)(R12//R3)
\(\left\{{}\begin{matrix}I3=U3:R3=6:60=0,1A\\I12=I1=I2=U12:R12=6:\left(80+40\right)=0,05A\left(R1ntR2\right)\end{matrix}\right.\)
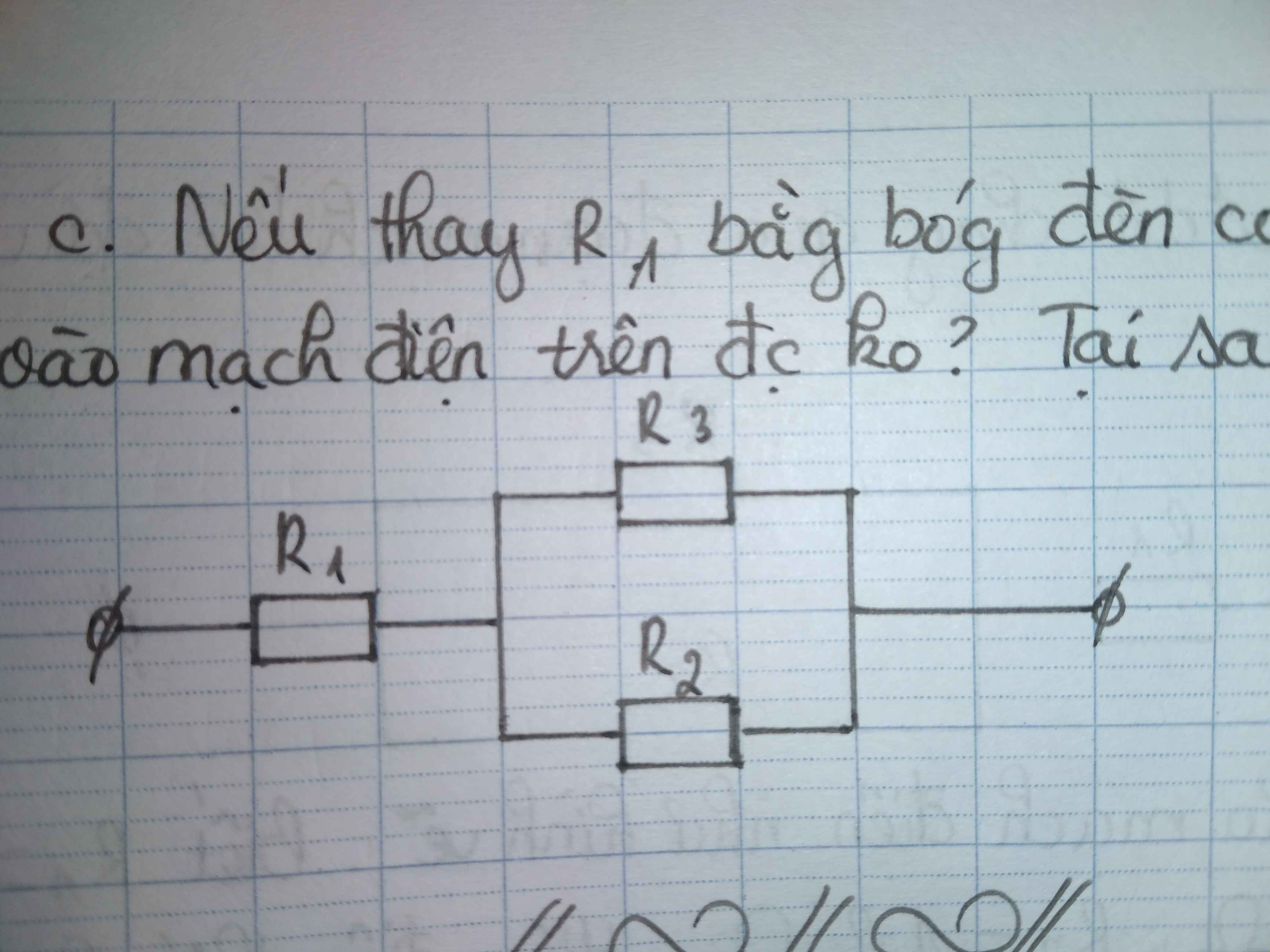
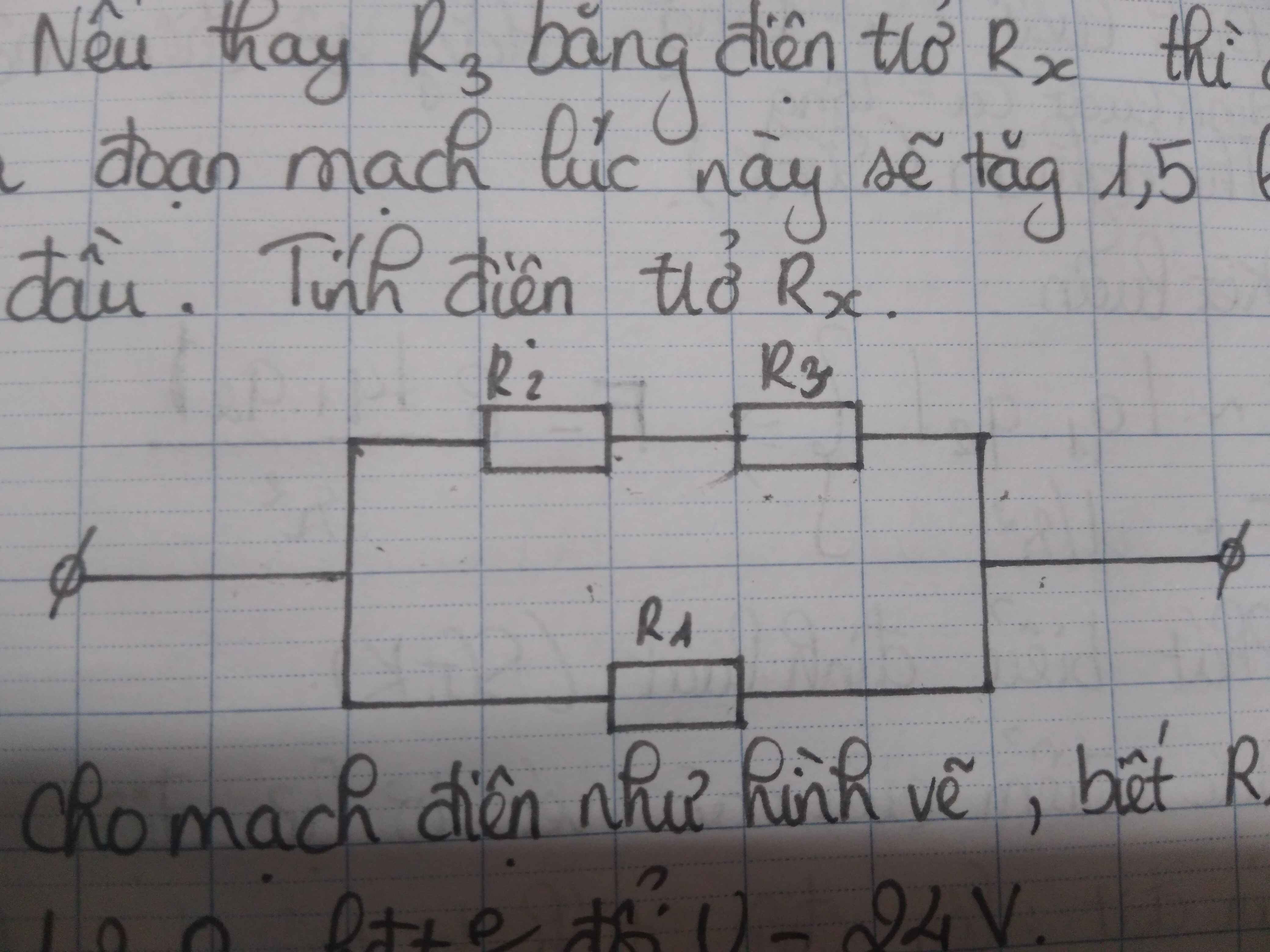
\(MCD:\left(R2//R3\right)ntR1\)
\(\rightarrow R=\dfrac{R2\cdot R3}{R2+R3}+R1=\dfrac{10\cdot12}{10+12}+10=\dfrac{170}{11}\Omega\)
\(I=I1=I23=U:R=24:\dfrac{170}{11}=\dfrac{132}{85}A\)
\(\rightarrow U1=I1\cdot R1=\dfrac{132}{85}\cdot10=\dfrac{264}{17}V\)
\(\rightarrow U23=U2=U3=U-U1=24-\dfrac{264}{17}=\dfrac{144}{17}V\)
\(\rightarrow\left\{{}\begin{matrix}I2=U2:R2=\dfrac{144}{17}:10=\dfrac{72}{85}A\\I3=U3:R3=\dfrac{144}{17}:12=\dfrac{12}{17}A\end{matrix}\right.\)