Question

[Đỗ Thạch Ngọc Anh]

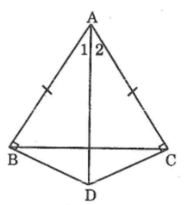
cho tam giác ABC cân tại A,góc A nhọn,các đường trung trực của AB,AC cắt nhau tại O.Vẽ hình.

a,chứng minh AO là tia phân giác của góc A

b,qua B kẻ đường thẳng vuông góc với AB,qua C kẻ đường thẳng vuông góc với AC chúng cắt nhau tai K

c,kẻ BD vuông góc với AC,CE vuông góc với AB,BD cắt CE tại H.chứng minh A,O,H,K thẳng hàng

Answer 1

[Nguyễn Lê Phước Thịnh]

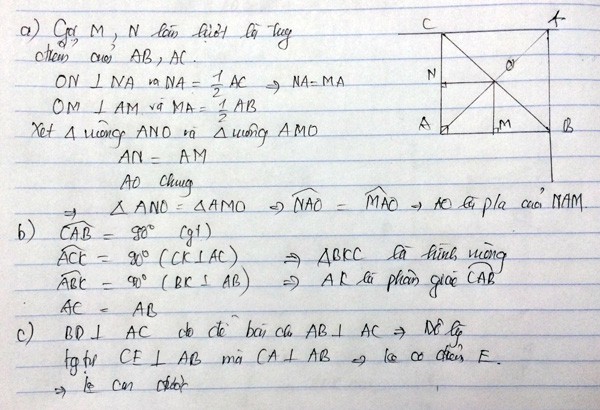
a) Gọi G, F lần lượt là chân đường vuông góc từ O kẻ xuống AB và AC

Ta có: O nằm trên đường trung trực của AB(gt)

mà OG⊥AB(gt)

nên G là trung điểm của AB

Ta có: O nằm trên đường trung trực của AC(gt)

mà OF⊥AC(gt)

nên F là trung điểm của AC

Ta có: \(AG=\dfrac{AB}{2}\)(G là trung điểm của AB)

\(AF=\dfrac{AC}{2}\)(F là trung điểm của AC)

mà AB=AC(ΔABC cân tại A)

nên AG=AF

Xét ΔAGO vuông tại G và ΔAFO vuông tại F có 

AO chung

AG=AF(cmt)

Do đó: ΔAGO=ΔAFO(cạnh huyền-cạnh góc vuông)

Suy ra: \(\widehat{GAO}=\widehat{FAO}\)(hai góc tương ứng)

hay \(\widehat{BAO}=\widehat{CAO}\)

mà tia AO nằm giữa hai tia AB,AC

nên AO là tia phân giác của \(\widehat{BAC}\)(đpcm)

c) Xét ΔAOB và ΔAOC có 

AB=AC(ΔABC cân tại A)

\(\widehat{BAO}=\widehat{CAO}\)(cmt)

AO chung

Do đó: ΔAOB=ΔAOC(c-g-c)

Suy ra: OB=OC(hai cạnh tương ứng)

Ta có: \(\widehat{ABC}+\widehat{KBC}=\widehat{ABK}\)(tia BC nằm giữa hai tia BA,BK)

nên \(\widehat{ABC}+\widehat{KBC}=90^0\)(1)

Ta có: \(\widehat{ACB}+\widehat{KCB}=\widehat{ACK}\)(tia CB nằm giữa hai tia CA,CK)

nên \(\widehat{ACB}+\widehat{KCB}=90^0\)(2)

Từ (1) và (2) suy ra \(\widehat{ABC}+\widehat{KBC}=\widehat{ACB}+\widehat{KCB}\)

mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)

nên \(\widehat{KBC}=\widehat{KCB}\)

Xét ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)(cmt)

nên ΔKBC cân tại K(Định lí đảo của tam giác cân)

Suy ra: KB=KC(hai cạnh bên)

Xét ΔBEC vuông tại E và ΔCDB vuông tại D có 

BC chung

\(\widehat{EBC}=\widehat{DCB}\)(hai góc ở đáy của ΔABC cân tại A)

Do đó: ΔBEC=ΔCDB(cạnh huyền-góc nhọn)

Suy ra: \(\widehat{BCE}=\widehat{CBD}\)(hai góc tương ứng)

hay \(\widehat{HBC}=\widehat{HCB}\)

Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)(cmt)

nên ΔHBC cân tại H(Định lí đảo của tam giác cân)

Suy ra: HB=HC(hai cạnh bên)

Ta có: AB=AC(ΔABC cân tại A)

nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)

Ta có: OB=OC(cmt)

nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)

Ta có: HB=HC(cmt)

nên H nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)

Ta có: KB=KC(cmt)

nên K nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(6)

Từ (3), (4), (5) và (6) suy ra A,O,H,K thẳng hàng(đpcm)