Cho mạch điện như hình, trong đó U = 12V, R1 = 1,5 ôm. Biết hiệu
điện thế hai đầu R1 là 6V. Tính nhiệt lượng tỏa ra trên R1 trong 2 phút ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
9 tháng 10 2018
Chọn đáp án B.
Vì
R 1 n t R 2 ⇒ U 1 = U - U 2 = 3 V ⇒ I 1 = I 2 = U 1 R 1 = 2 A
Điện trở R 2 là R 2 = R - R 1 = 9 2 - 1 , 5 = 3 Ω
Nhiệt lượng tỏa ra trên ,trong thời gian 2 phút (120 giây)là:
Q = I 2 2 R 2 t = 2 2 . 3 . 120 = 1440 J
HT
13 tháng 1 2021
\(R_D=\dfrac{U_{dm}^2}{P_{dm}}=\dfrac{36}{6}=6\left(\Omega\right)\)
\(R_DntR_1\Rightarrow R_{td}=R_1+R_D=3+6=9\left(\Omega\right)\)
\(I=I_{dm}=\dfrac{P_{dm}}{U_{dm}}=\dfrac{6}{6}=1\left(A\right)\)
\(\Rightarrow U_1=I.R_1=1.3=3\left(V\right)\)
\(Q=I^2.R_{td}.t=1.9.5.60=2700\left(J\right)\)
26 tháng 9 2021
a) Điện trở tương đương Rtđ(1):
\(R_{tđ\left(1\right)}=R_1+R_2=20+30=50\left(\Omega\right)\)
ĐTTĐ của mạch:
\(R_{tđ}=\dfrac{R_{tđ\left(1\right)}.R_3}{R_{tđ\left(1\right)}+R_3}=\dfrac{50.30}{50+30}=18,75\left(\Omega\right)\)
b, CĐDĐ toàn mạch:
\(I=\dfrac{U}{R}=\dfrac{60}{18,75}=3,2\left(A\right)\)
DK
25 tháng 10 2023
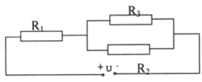
Câu 2:
a) R\(_{tđ}\) = \(\dfrac{R_1.R_2}{R_1+R_2}\) = \(\dfrac{20.60}{20+60}\) = 15 ( ÔM )
b)
I = \(\dfrac{U}{R_{TĐ}}\) = \(\dfrac{12}{15}\) = 0,8 ( V)
\(\Rightarrow\) I\(_1\) = \(\dfrac{U}{R_1}\) = \(\dfrac{12}{20}\) = 0,6 ( A)
\(\Rightarrow\) \(I_2\) = \(\dfrac{U}{R_2}\) = \(\dfrac{12}{60}\) = 0,2 ( A)
c) \(P_2\) = U.I\(_2\) = 12 . 0,2 = 2,4 ( W)
d) \(A_{AB}\) = U.I .t= 120.12.0,8 = 1152 ( J )
DK
25 tháng 10 2023
Câu 1:
a) R\(_{tđ}\) = R\(_1\) + R\(_2\) = 16 + 24 = 40 ( ôm )
\(\Rightarrow\)I = \(\dfrac{U_{MN}}{R_{tđ}}\) = \(\dfrac{36}{40}\) = 0,9 ( A )
I = I\(_1\) = I\(_2\) = 0,9 A
U\(_1\) = I . R \(_1\)= 16 . 0,9 =14,4 ( V)
U\(_2\) = I . R\(_2\) = 24 . 0,9 = 21,6 ( V )
b) P = U . I = 36 . 0,9 = 32,4 ( W )
c) P\(_1\)= U\(_1\) . I = 14,4 . 0,9 = 12,96 ( W)
Đổi 12 phút = 720 giây
A\(_1\) = P\(_1\) . t = 720 . 12,96 = 9331,2 (J)
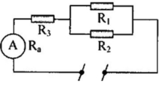
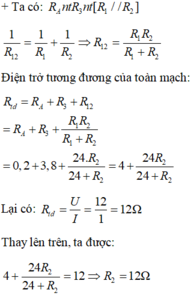
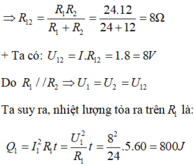
\(Q_{tỏa}=RI^2t=1,5\cdot\left(\dfrac{6}{1,5}\right)^2\cdot2\cdot60=2880J\)