Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Áp dụng định lí cosin trong tam giác ta có:
AB2 = AC2 + BC2 - 2BC.AC.cosC
= 2502 + 1202 - 2.250.120.cos78024’ = 64835
Suy ra AB = 255.

Ta có thể dùng nhiều kim nam châm thử đặt xung quanh một nam châm lớn, sự định hướng của các kim nam châm thử cho ta hình ảnh của từ trường.

Đáp án A
Cây trắng này xuất hiện với tần số 1: 1000 nên cây này xuất hiện do đột biến như là mất đoạn NST mang gen quy định hoa đỏ A nên tạo ra hiện tượng giả trội

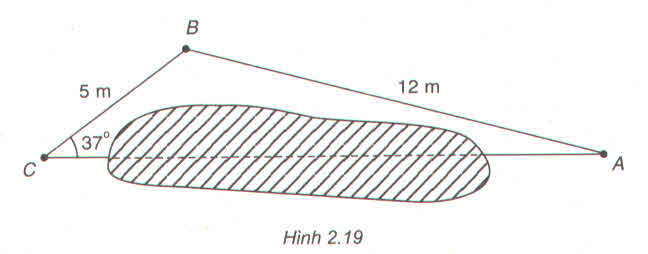
Hạ \(BH\perp AC\).
\(CH=CB.sin37^o\approx3m.\)
Áp dụng định lý Pi-ta-go trong tam giác vuông BCH:
\(BH=\sqrt{AB^2-AH^2}=\sqrt{5^2-3^2}=4m\).
Áp dụng định lý Pi-ta-go trong tam giác vuông BHA:
\(HA=\sqrt{BC^2-BH^2}=\sqrt{12^2-4^2}=8\sqrt{2}m\).
\(AC=AH+HC=8\sqrt{2}+3m\).

Khi người đi bộ ngồi nghỉ -> Người đi bộ đã đi được : 5 . 2 = 10 ( km )
Người xe đạp đi được quãng đường trong 1h :
\(15.1=15\left(\dfrac{km}{h}\right)=\dfrac{3}{4}AC\)
Gọi tg người đi xe đạp từ A đến B là : a (h)
-> \(AB=15a\left(km\right)\)
- (t) người đi bộ đi từ C -> B là : a+1 (h)
- CD = 10 km
- (t) người đi bộ từ D đến B là : \(\left(a+1\right)-2-0,5=a-1,5\left(h\right)\)
\(\Rightarrow DB=5.\left(a-1,5\right)\left(km\right)\)
\(\Rightarrow BC=CD+DB=10+5.\left(a-1,5\right)=5a+2,5\left(km\right)\)
Có AC + BC = AB
\(\Rightarrow20+5a+2,5=15a\)
\(\Rightarrow22,5=10a\)
\(\Rightarrow a=2,25\left(h\right)\)
\(AB=15a=15.2,25=33,75\left(km\right)\)
\(AD=AC+CD=20+10=30\left(km\right)\)
Để gặp người đi bộ chỗ ngồi nghỉ thì : tg đi từ A->D thuộc ( 1 ; 15 )
\(\rightarrow1\le\dfrac{30}{v_2}\le1,5\)
\(\Rightarrow30\ge v_2\ge20\left(\dfrac{km}{h}\right)\)

a)QĐ AC dài là
Sac=15.1.3/4=20km
Khi người đi bộ ngồi nghỉ người đi XĐ đi Dc QĐ Là
s1=15.0.5=7,5km
QĐ người đi XĐ đi đc là
S2=5.2=10km
Khi đó,K/c giữa 2 xe là
s3=s2-S1=5.2=10km
2,5+v1t==v2t
2,5+5t=15t
=>10t=2,5=>t=0,25
=>Sbc=10+2,5+0,25.5=13,75km
=>Sab=20+13,5=33,75km

định lý cosin: \(AB=\sqrt{CA^2+CB^2-2CACB\cos\left(78^024'\right)}\)
Tự thay số nốt