phân tích thành nhân tử x7+x2+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
2
3 tháng 8 2015
Bài 1 :
\(x^2-6x+8=x^2-2x-4x+8=x\left(x-2\right)-4\left(x-2\right)=\left(x-4\right)\left(x-2\right)\)
Bài 2 :
\(x^8+x^7+1=x^8+x^7+x^6+x^5+x^4+x^3+x^2+x+1-x^6-x^5-x^4-x^3-x^2-x\)
\(=x^6\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)+x^2+x+1-x^4\left(x^2+x+1\right)-x\left(x^2+x+1\right)\)
=\(\left(x^2+x+1\right)\left(x^6+x^3+1-x^4-x\right)\)
Tick đúng nha
PN
1
11 tháng 10 2021
\(3x\left(x+1\right)^2-5x^2\left(x+1\right)+7\left(x+1\right)\)
\(=\left(x+1\right)\left(3x^2+3x-5x^2+7\right)\)
\(=\left(x+1\right)\left(-2x^2+3x+7\right)\)
AN
2 tháng 10 2017
x7 + x2 + 1 = (x7 – x) + (x2 + x + 1)
= x.(x6 – 1) + (x2 + x +1)
= x.(x3 - 1).(x3 +1) + (x2 + x +1)
= x.(x-1).(x2 + x +1).(x3 +1) + (x2 + x +1)
= (x2 + x +1).[x.(x-1).(x3 +1) + 1]
= (x2 + x +1).[(x2-x).(x3 +1) + 1]
= (x2 + x +1).(x5-x4 + x2 -x + 1)
TT
4
7 tháng 10 2023
\(f\left(x\right)=x^7+x^2+1\)
\(f\left(x\right)=\left(x^7-x\right)+\left(x^2+x+1\right)\)
\(f\left(x\right)=x\left(x^6-1\right)+\left(x^2+x+1\right)\)
\(f\left(x\right)=x\left(x^3-1\right)\left(x^3+1\right)+\left(x^2+x+1\right)\)
\(f\left(x\right)=x\left(x-1\right)\left(x^2+x+1\right)\left(x^3+1\right)+\left(x^2+x+1\right)\)
\(f\left(x\right)=\left(x^2+x+1\right)\left(x^5-x^4+x^2-x+1\right)\)
Xét đa thức \(g\left(x\right)=x^5-x^4+x^2-x+1\). Giả sử đa thức này có nghiệm hữu tỉ \(x=\dfrac{p}{q}\left(p,q\inℤ;\left(p,q\right)=1\right)\) thì \(p|1,q|1\) nên \(x=\pm1\). Thử lại, ta thấy cả 2 nghiệm này đều không thỏa mãn. Do đó đa thức g(x) không thể có nghiệm hữu tỉ. (*)
Giả sử ta có thể phân tích tiếp \(g\left(x\right)\) thành nhân tử thì \(g\left(x\right)=h\left(x\right).j\left(x\right)\) với h(x) và j(x) là các đa thức hệ số hữu tỉ khác hằng có bậc nhỏ hơn 5 thì một trong 2 đa thức h(x), j(x) phải có bậc lẻ (vì nếu cả 2 cùng có bậc chẵn thì \(g\left(x\right)=h\left(x\right).j\left(x\right)\) sẽ có bậc chẵn, vô lí). Mà một đa thức bậc lẻ thì luôn có nghiệm nên nếu g(x) phân tích được thành nhân tử thì nó sẽ có nghiệm hữu tỉ, mâu thuẫn với (*).
Vậy ta không thể phân tích tiếp g(x) thành nhân tử. Điều này có nghĩa rằng ta đã hoàn thành xong việc phân tích f(x) thành nhân tử.
HN
0
NN
0
ND
1
28 tháng 1 2019
\(A=\left(x-1\right)\left(x-2\right)\left(x+7\right)\left(x+8\right)+8\)
\(A=\left[\left(x-1\right)\left(x+7\right)\right]\left[\left(x-2\right)\left(x+8\right)\right]+8\)
\(A=\left(x^2+6x-7\right)\left(x^2+6x-16\right)+8\)
Đặt \(q=x^2+6x-7\)ta có :
\(A=q\left(q-9\right)+8\)
\(A=q^2-9q+8\)
\(A=q^2-q-8q+8\)
\(A=q\left(q-1\right)-8\left(q-1\right)\)
\(A=\left(q-1\right)\left(q-8\right)\)
Thay \(q=x^2+6x-7\)vào A ta được :
\(A=\left(x^2+6x-7-1\right)\left(x^2+6x-7-8\right)\)
\(A=\left(x^2+6x-8\right)\left(x^2+6x-15\right)\)
SH
0
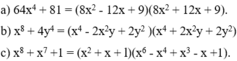
Có nhân tử x2+x+1