Một con lắc lò xo dao động điều hòa. Biết lò xo có độ cứng 100 N/m và vật nhỏ có khối lượng 100g. Lấy p2 = 10. Động năng của con lắc biến thiên tuần hoàn theo thời gian với tần số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Phương pháp: Động năng của con lắc biến thiên tuần hoàn theo thời gian với tần số bằng hai lần tần số của vật dao động điều hoà
Cách giải :
Động năng của con lắc biến thiên tuần hoàn theo thời gian với tần số
f = 2 . 1 2 π = k m = 6 Hz

Đáp án A
Phương pháp: Động năng của con lắc biến thiên theo thời gian với tần số bằng 2 lần tần số của dao động điều hoà
Cách giải:
Gọi f là tần số dao động của con lắc thì động năng của con lắc biến thiên theo thời gian với tần số 2f
Tần số dao động: f = 1 2 π k m = 1 2 π 36 0 , 1 = 3 Hz
Vậy động năng của con lắc biến thiên theo thời gian với tần số f’ = 2.3 = 6Hz

Đáp án A.
Vì động năng của con lắc biến thiên với tần số ω ' = 2 ω hay f ' = 2 f
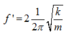
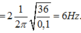

Đáp án A
+ Tần số góc của dao động f = 1 2 π k m = 3 Hz, vậy động năng của con lắc sẽ biến thiên với tần số 6 Hz

Đáp án A
Tần số góc của dao động 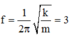 Hz → động năng biến thiên với tần số 6 Hz
Hz → động năng biến thiên với tần số 6 Hz
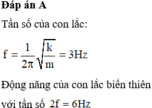

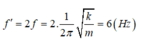
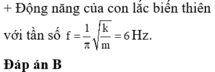
\(x=A\cos\left(\omega t+\varphi\right)\Rightarrow x'=v=\omega A\sin\left(\omega t+\varphi\right)\)
\(W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}.m.\omega^2A^2\sin^2\left(\omega t+\varphi\right)\)
\(=\dfrac{1}{2}kA^2.\dfrac{1}{2}\left[1-\cos2\left(\omega t+\varphi\right)\right]\)
\(=\dfrac{1}{4}kA^2\left[1-\cos\left(2\omega t+2\varphi\right)\right]\)
\(\Rightarrow f_{W_d}=2f_x=2.\dfrac{\omega}{2\pi}=\sqrt{\dfrac{k}{m.\pi^2}}=10\left(Hz\right)\)