Bài 31:Cho đường tròn (O), đường kính MN và dây cung PQ vuông gócvới MN tại I ( khác M, N). Trên cung nhỏ NP lấy điểm J (khác N, P). Nối M với J cắt PQ tại H.a) Chứng minh 4 điểm H, I, N, J cùng nằm trên một đường trònb) Gọi giao điểm của PN với MJ là G; JQ với MN là K. Chứng minh: GK // PQ.c) Chứng minh G là tâm đường tròn nội tiếp DPKJ.d) JN cắt PQ tại A. Tính: HP.AQ -...
Đọc tiếp
Bài 31:Cho đường tròn (O), đường kính MN và dây cung PQ vuông gócvới MN tại I ( khác M, N). Trên cung nhỏ NP lấy điểm J (khác N, P). Nối M với J cắt PQ tại H.
a) Chứng minh 4 điểm H, I, N, J cùng nằm trên một đường tròn
b) Gọi giao điểm của PN với MJ là G; JQ với MN là K. Chứng minh: GK // PQ.
c) Chứng minh G là tâm đường tròn nội tiếp DPKJ.
d) JN cắt PQ tại A. Tính: HP.AQ - AP.HQ
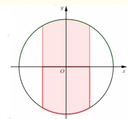Chọn hệ trục tọa độ Oxy như hình vẽ với O là gốc tọa độ. Phương trình đường tròn tâm O, đường kính AB = 8 là
x
2
+
y
2
=
16
⇔
y
2
=
16
-
x
2
⇔
x
=
±
16
-
x
2
.
a) Xét (O) có
ΔMJN nội tiếp đường tròn(M,J,N∈(O))
MN là đường kính(gt)
Do đó: ΔMJN vuông tại J(Định lí)
⇒\(\widehat{MJN}=90^0\)
⇔\(\widehat{HJN}=90^0\)
Xét tứ giác HJNI có
\(\widehat{HJN}\) và \(\widehat{HIN}\) là hai góc đối
\(\widehat{HJN}+\widehat{HIN}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: HJNI là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
⇔H,J,N,I cùng nằm trên một đường tròn