cho đtròn tâm O, đường kính AB=2R. lấy điểm c trên đtròn. Trên cùng 1 nửa mặt phẳng bờ AB chứa điểm C dựng 2 tia Ax và By cùng vuông góc với AB. Qua điểm C dựng tiếp tuyến với đtròn cắt tia Ax và By lần lượt tại M và N.
a.cm 4 điểm M, C, O, A cùng nằm trên 1 đtròn
b. cm góc CMO bằng góc CAO.
c. cm BC.MN=2R.ON
(gợi ý;: cm 2 tam giác vuông đồng dạng , 2R là đường kính của đtròn.)
d. khi AM = \(R\sqrt{3}\) hãy tính tỉ số diện tích của tm giác ACB và tam giác MON.


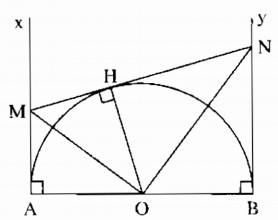


a) Xét tứ giác AOCM có
\(\widehat{MAO}\) và \(\widehat{MCO}\) là hai góc đối
\(\widehat{MAO}+\widehat{MCO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AOCM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
nên A,O,C,M cùng nằm trên một đường tròn(đpcm)