tính tổng cấp số nhân vô hạn \(\dfrac{1}{2};-\dfrac{1}{4};\dfrac{1}{8};...;\dfrac{\left(-1\right)^{n+1}}{2^n};...\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2021
Cấp số nhân lùi vô hạn có \(u_1=1\) và \(q=\dfrac{1}{2}\)
\(\Rightarrow S=\dfrac{u_1}{1-q}=\dfrac{1}{1-\dfrac{1}{2}}=2\)

13 tháng 7 2023
a: \(S=\dfrac{\dfrac{2}{3}}{\dfrac{5}{4}}=\dfrac{8}{15}\)
b: 1,(6)=5/3

CM
19 tháng 6 2019
a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
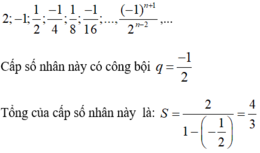


CM
14 tháng 7 2017
Đáp án B
- Cách giải:
Cho cấp số nhân lùi vô hạn
u
n
có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức 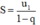

HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) \(S = \frac{{{u_1}}}{{1 - q}} = \frac{{\frac{2}{3}}}{{1 - \frac{{ - 1}}{4}}} = \frac{8}{{15}}\)
b) \(1,\left( 6 \right) = \frac{5}{3}\)

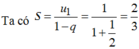
\(\left\{{}\begin{matrix}u_1=\dfrac{1}{2}\\q=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow S=\dfrac{1}{2}.\dfrac{1}{1+\dfrac{1}{2}}=\dfrac{1}{3}\)