Giải phương trình: (x2 + x + 1)(x2 + x + 2) = 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CB
1
AH
Akai Haruma
Giáo viên
12 tháng 2 2023
Lời giải:
Đặt $x^2+x=a$ thì pt trở thành:
$(a-2)(a-3)=12$
$\Leftrightarrow a^2-5a+6=12$
$\Leftrightarrow a^2-5a-6=0$
$\Leftrightarrow (a+1)(a-6)=0$
$\Leftrightarrow a+1=0$ hoặc $a-6=0$
$\Leftrightarrow x^2+x+1=0$ hoặc $x^2+x-6=0$
Nếu $x^2+x+1=0$
$\Leftrightarrow (x+\frac{1}{2})^2=-\frac{3}{4}<0$ (vô lý - loại)
Nếu $x^2+x-6=0$
$\Leftrightarrow (x-2)(x+3)=0$
$\Leftrightarrow x=2$ hoặc $x=-3$
PT
1
CM
13 tháng 12 2018
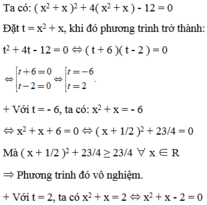
⇔ ( x + 2 )( x - 1 ) = 0 ⇔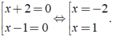 
Vậy phương trình có tập nghiệm là S = { - 2;1 }.
AH
Akai Haruma
Giáo viên
24 tháng 8 2023
1. Đặt $x^2+x=a$ thì pt trở thành:
$a^2+4a=12$
$\Leftrightarrow a^2+4a-12=0$
$\Leftrightarrow (a-2)(a+6)=0$
$\Leftrightarrow a-2=0$ hoặc $x+6=0$
$\Leftrightarrow x^2+x-2=0$ hoặc $x^2+x+6=0$
Dễ thấy $x^2+x+6=0$ vô nghiệm.
$\Rightarrow x^2+x-2=0$
$\Leftrightarrow (x-1)(x+2)=0$
$\Leftrightarrow x=1$ hoặc $x=-2$
AH
Akai Haruma
Giáo viên
24 tháng 8 2023
2.
$x(x-1)(x+1)(x+2)=24$
$\Leftrightarrow [x(x+1)][(x-1)(x+2)]=24$
$\Leftrightarrow (x^2+x)(x^2+x-2)=24$
$\Leftrightarrow a(a-2)=24$ (đặt $x^2+x=a$)
$\Leftrightarrow a^2-2a-24=0$
$\Leftrightarrow (a+4)(a-6)=0$
$\Leftrightarrow a+4=0$ hoặc $a-6=0$
$\Leftrightarrow x^2+x+4=0$ hoặc $x^2+x-6=0$
Nếu $x^2+x+4=0$
$\Leftrightarrow (x+\frac{1}{2})^2=\frac{1}{4}-4<0$ (vô lý - loại)
Nếu $x^2+x-6=0$
$\Leftrightarrow (x-2)(x+3)=0$
$\Leftrightarrow x-2=0$ hoặc $x+3=0$
$\Leftrightarrow x=2$ hoặc $x=-3$
N
1
21 tháng 3 2021
\(\dfrac{1}{x+2}\)+\(\dfrac{5}{x-2}\)=\(\dfrac{2x-12}{x^2-4}\)
(đkxđ: x≠2, x≠-2)
⇔ \(\dfrac{x-2}{x^2-4}\)+\(\dfrac{5\left(x+2\right)}{x^2-4}\)= \(\dfrac{2x-12}{x^2-4}\)
⇔ x-2+5(x+2)=2x-12
⇔ x-2+5x+10=2x-12
⇔ 4x=-20
⇔ x=-5(tm)
PT
1
CM
29 tháng 5 2018
Ta có: 3 x 2 + 4(x – 1) = x - 1 2 + 3
⇔ 3 x 2 + 4x – 4 = x 2 – 2x + 1 + 3
⇔ 2 x 2 + 6x – 8 = 0 ⇔ x 2 + 3x – 4 = 0
Phương trình x 2 + 3x – 4 = 0 có hệ số a = 1, b = 3, c = -4 nên có dạng a + b + c = 0, suy ra x 1 = 1, x 2 = -4
Vậy phương trình đã cho có hai nghiệm x 1 = 1, x 2 = -4
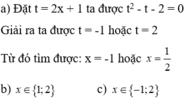
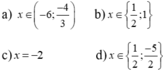
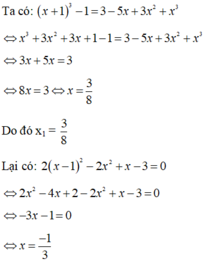
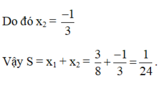
\(\left(x^2+x+1\right)\left(x^2+x+2\right)=12\)
Đặt \(x^2+x+1=t\)
\(\Leftrightarrow t\left(t+1\right)=12\Leftrightarrow t^2+t-12=0\)
\(\Leftrightarrow\left(t-3\right)\left(t+4\right)=0\)
\(\Leftrightarrow\left(x^2+x-2\right)\left(x^2+x+5\ne0\right)=0\)( tự chứng minh )
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow x=1;x=-2\)
Vậy tập nghiệm phương trình là S = { 1 ; -2 }