Giá trị nhỏ nhất của biểu thức P=4x+16\x^2, x>0 bằng bao nhiêu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


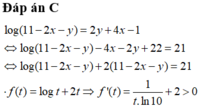
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

Đáp án C
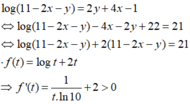
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

a, Với x = 1015 , ta có :
\(A=\frac{2002-1998:(1015-16)}{316+6,84:0,01}\)
\(A=\frac{2002-1998:999}{316+\frac{684}{100}:\frac{1}{100}}\)
\(A=\frac{2002-2}{316+\frac{171}{25}\cdot100}\)
\(A=\frac{2000}{316+\frac{171}{1}\cdot4}\)
\(A=\frac{2000}{316+684}=\frac{2000}{1000}=2\)
b, Tự làm

\(M=\)như trên
\(=>M=4x^2-4x+1+x+\frac{1}{4x}+2010\)
\(=>M=\left(4x^2-4x+1\right)+\left(x+\frac{1}{4x}\right)+2010\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\)
Áp dụng BĐT Cô- si cho 2 số không âm, ta có:
\(x+\frac{1}{4x}\ge2\sqrt{x.\frac{1}{4x}}=2\sqrt{\frac{1}{4}}=1\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\ge0+1+2010=2011\\ \)
=>minM=2011 khi x=\(\frac{1}{2}\)

\(B=\frac{x^2+4x+85}{3\left(x+2\right)}=\frac{\left(x^2-14x+49\right)+\left(18x+36\right)}{3\left(x+2\right)}\)
\(=\frac{\left(x-7\right)^2+18\left(x+2\right)}{3\left(x+2\right)}=\frac{\left(x-7\right)^2}{3\left(x+2\right)}+6\ge6\forall x>0\)
Dấu "=" xảy ra khi: \(x-7=0\Leftrightarrow x=7\)




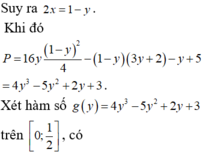
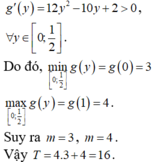
Có : \(P=4x+\dfrac{16}{x^2}=2x+2x+\dfrac{16}{x^2}\)
- AD AMGM : \(2x+2x+\dfrac{16}{x^2}\ge3\sqrt[3]{\dfrac{2x.2x.16}{x^2}}=12\)
- Dấu " = " xảy ra \(\Leftrightarrow2x=\dfrac{16}{x^2}\)
\(\Leftrightarrow2x^3=16\)
\(\Leftrightarrow x=2\) ( TM )
Vậy ....
( Chắc đề như vầy :vvv )
Dùng cái này đánh công thức nha bạn