Cho tam giác ABC gọi I là tâm đường tròn nội tiếp tam giác ABC, biết \(IG\perp IC\). CMR \(\dfrac{a+b+c}{3}=\dfrac{2ab}{a+b}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


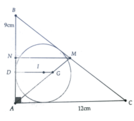
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm

Tham khảo:
Ta có: \(R=\dfrac{abc}{4S};r=\dfrac{S}{p}\)
Vì tam giác ABC vuông cân tại A nên \(b=c\) và \(a=\sqrt{b^2+c^2}=b\sqrt{2}\)
Xét tỉ số:
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}.\left(b.c\right)^2}=\dfrac{a\left(a+2b\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)

Kẻ đường phân giác CJ của góc ACP cắt PE tại R mà không nói rõ J thuộc đương thẳng nào? đề khó hỉu quá anh(chị) ơi
a) Do P đối xứng B qua AC \(\Rightarrow\) \(\Delta\)APC đối xứng \(\Delta\)ABC qua AC \(\Rightarrow\) CR đối xứng CS qua AC ( vì CS là phân giác góc ACB) \(\Leftrightarrow\) R đối xứng S qua AC \(\Leftrightarrow\) RS\(\perp\)AC mà PB\(\perp\)AC \(\Leftrightarrow\) RS//PB
b) Do K đối xứng P qua CJ \(\Rightarrow\) CK đối xứng CP qua CJ \(\Leftrightarrow\) góc JCK = góc JCP = góc JCA ( vì CJ là phân giác góc ACP) \(\Rightarrow\)tia CK trùng tia CA \(\Rightarrow\) C; A; K thẳng hàng (1)
Cũng Do K đối xứng P qua CJ hay CR nên từ (1) \(\Rightarrow\) góc AKR = góc CKR = góc CPR = góc APR (2) ( vì PR là phân giác góc APC do BS là phân giác góc ABC vì \(\Delta\)APC đối xứng \(\Delta\)ABC qua AC)
Từ (2) \(\Rightarrow\) AKPR nội tiếp \(\Rightarrow\) AKBS nội tiếp ( vì đối xứng)
c) Gọi M là giao điểm của 2 tiếp tuyến tại K,P của (O) ⇒\(\Rightarrow\)M \(\in\) trung trực của KP (3)
Do K đối xứng P qua CJ \(\Leftrightarrow\) CJ là trung trực của KP (4)
Từ (3) và (4) ⇒ 2 tiếp tuyến tại K,P của (O) và CJ đồng quy tại M
ĐS:..................( đến đây thôi vì đề hơi kì xíu)
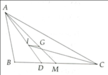


G là trọng tâm à bạn?