Giải phương trình: x4−8x3+21x2−24x+9=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(x^4-8x^3+21x^2-24x+9=0\)
\(\Leftrightarrow x^4-5x^3+3x^2-3x^3+15x^2-9x+3x^2-5x+9=0\)
\(\Leftrightarrow\left(x^2-5x+3\right)\left(x^2-3x+3\right)=0\)
\(\Leftrightarrow x^2-5x+3=0\)
\(\text{Δ}=\left(-5\right)^2-4\cdot1\cdot3=25-12=13\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5-\sqrt{13}}{2}\\x_2=\dfrac{5+\sqrt{13}}{2}\end{matrix}\right.\)

Đặt m = x 2 .Điều kiện m ≥ 0
Ta có: x 4 -8 x 2 – 9 =0 ⇔ m 2 -8m -9 =0
Phương trình m 2 - 8m - 9 = 0 có hệ số a = 1,b = -8,c = -9 nên có dạng a – b + c = 0
suy ra: m 1 = -1 (loại) , m 2 = -(-9)/1 =9
Ta có: x 2 =9 ⇒ x= ± 3
Vậy phương trình đã cho có 2 nghiệm : x 1 =3 ; x 2 =-3

\(\sqrt{16x^2+9-24x}-17=0\)
\(\Leftrightarrow\sqrt{16x^2+9-24x}=17\)
\(\Leftrightarrow16x^2-24x+9=289\)
\(\Leftrightarrow16x^2-24x-280=0\)
\(\Leftrightarrow16x^2-80x+56x-280=0\)
\(\Leftrightarrow16x\left(x-5\right)+56\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(16x+56\right)=0\)
\(\Leftrightarrow8\left(x-5\right)\left(2x+7\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-5=0\\2x+7=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=5\\x=\frac{-7}{2}\end{cases}}\)
Vậy ...

nhận thấy x = 0 không là nghiệm của phương trình
Chia 2 vế phương trình cho x2, ta được :
\(x^2-9x+24-\frac{27}{x}+\frac{9}{x^2}=0\) ( 1 )
đặt \(t=x+\frac{3}{x}\)
( 1 ) \(\Leftrightarrow\left(x+\frac{3}{x}\right)^2-9\left(x+\frac{3}{x}\right)+18=0\)
\(\Leftrightarrow t^2-9t+18=0\Leftrightarrow\left(t-6\right)\left(t-3\right)=0\Leftrightarrow\orbr{\begin{cases}t=6\\t=3\end{cases}}\)
Khi đó : \(\orbr{\begin{cases}x+\frac{3}{x}=6\Leftrightarrow x=3\pm\sqrt{6}\\x+\frac{3}{x}=3\Leftrightarrow x\in\varnothing\end{cases}}\)

ta có:
x4-8x2-9=0
x4+9x2-x2-9=0
x4-x2+9x2-9=0
x2(x2-1)+9(x2-10=0
(x2-1)(x2+9)=0
=>x2-1=0=>x=1
=>x2+9=0=>x=-3

Chọn đáp án C.
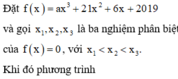
4 a x 3 + 21 x 2 + 6 x + 2019 3 a x + 21 = 9 a x 2 + 14 x + 2 2
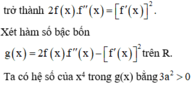
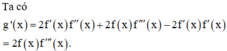
Vì f(x) = 0 có ba nghiệm phân biệt nên a ≠ 0
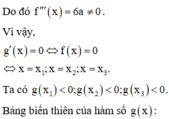
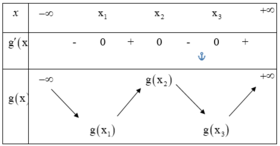
Từ bảng biến thiên, ta thấy phương trình g(x) = 0 có đúng hại nghiệm phân biệt.
Do đó phương trình 4 a x 3 + 21 x 2 + 6 x + 2019 3 a x + 21 = 9 a x 2 + 14 x + 2 2 có đúng hai nghiệm phân biệt.

Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm 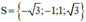
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
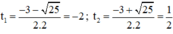
t 1 = - 2 < 0 nên loại.
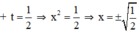
Vậy phương trình có tập nghiệm 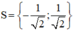
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
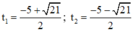
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.

Đáp án: A.
y' = 4 x 3 - 4x.
Tiếp tuyến phải tìm đi qua điểm có hoành độ thỏa mãn
4 x 3 - 4x = 24 ⇔ x 3 - x - 6 = 0 ⇔ (x - 2)( x 2 + 2x + 3) = 0 ⇔ x = 2.
Do đó phương trình tiếp tuyến phải tìm là
y - y(2) = 24(x - 2) ⇔ y = 24x - 43.

Đáp án: A.
y' = 4 x 3 - 4x.
Tiếp tuyến phải tìm đi qua điểm có hoành độ thỏa mãn
4 x 3 - 4x = 24 ⇔ x 3 - x - 6 = 0 ⇔ (x - 2)( x 2 + 2x + 3) = 0 ⇔ x = 2.
Do đó phương trình tiếp tuyến phải tìm là
y - y(2) = 24(x - 2) ⇔ y = 24x - 43.
Ta thấy với \(x=0\)thay vào phương trình ta có:
\(0-8.0+21.0-24.0+9=9\ne0\)
\(\Rightarrow x=0\)không là nghiệm của phương trình
Khi đó, chia cả 2 vế cho \(x^2\)ta được:
\(x^2-8x+21-24.\frac{1}{x}+\frac{9}{x^2}=0\)
\(\Leftrightarrow\left(x^2+6+\frac{9}{x^2}\right)-\left(8x+24.\frac{1}{x}\right)+15=0\)
\(\Leftrightarrow\left(x+\frac{3}{x}\right)^2-8\left(x+\frac{3}{x}\right)+15=0\)
Đặt \(x+\frac{3}{x}=t\)
\(\Rightarrow t^2-8t+15=0\)\(\Leftrightarrow t^2-3t-5t+15=0\)
\(\Leftrightarrow t\left(t-3\right)-5\left(t-3\right)=0\)\(\Leftrightarrow\left(t-3\right)\left(t-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t-3=0\\t-5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}t=3\\t=5\end{cases}}\)
+) Nếu \(t=3\)\(\Rightarrow x+\frac{3}{x}=3\)
\(\Rightarrow\frac{x^2+3}{x}=\frac{3x}{x}\)\(\Leftrightarrow x^2+3=3x\)
\(\Leftrightarrow x^2-3x+3=0\)\(\Leftrightarrow x^2-2.\frac{3}{2}x+\frac{9}{4}+\frac{3}{4}=0\)
\(\Leftrightarrow\left(x-\frac{3}{2}\right)^2+\frac{3}{4}=0\)
Vì \(\left(x-\frac{3}{2}\right)^2\ge0\)\(\forall x\)\(\Rightarrow\left(x-\frac{3}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
\(\Rightarrow\)Phương trình vô nghiệm
+) Nếu \(t=5\)\(\Leftrightarrow x+\frac{3}{x}=5\)\(\Leftrightarrow\frac{x^2+3}{x}=\frac{5x}{x}\)
\(\Leftrightarrow x^2+3=5x\)\(\Leftrightarrow x^2-5x+3=0\)
\(\Leftrightarrow x^2-2.\frac{5}{2}x+\frac{25}{4}-\frac{13}{4}=0\)
\(\Leftrightarrow\left(x-\frac{5}{2}\right)^2=\frac{13}{4}\)\(\Leftrightarrow\orbr{\begin{cases}x-\frac{5}{2}=\frac{-\sqrt{13}}{2}\\x-\frac{5}{2}=\frac{\sqrt{13}}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{5-\sqrt{13}}{2}\\x=\frac{5+\sqrt{13}}{2}\end{cases}}\)
Vậy tập nghiệm của phương trình là : \(S=\left\{\frac{5-\sqrt{13}}{2};\frac{5+\sqrt{13}}{2}\right\}\)