tính tổng tất cả các số hạng của một cấp số nhân có số hạng đầu bằng \(\sqrt{2}\), số hạng thứ 2 bằng \(-2\) và số hạng cuối là \(64\sqrt{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


u 1 = 18 , u 2 = 54 ⇒ q = u 2 u 1 = 3.
Lại có u n = 39366 ⇔ u 1 . q n − 1 = 39366 ⇔ 18.3 n − 1 = 39366 ⇔ 3 n − 1 = 3 7 ⇔ n = 8
Vậy S 8 = 18. 1 − 3 8 1 − 3 = 59040
Chọn đáp án B.

Chọn B.
u1 = 18, u2 = 54 ⇒ q = 3
un = 39366 ⇔ u1.qn-1 = 39366 ⇔ 18.3n-1 = 39366 ⇔ 3n-1 = 37 ⇔ n = 8.
Vậy 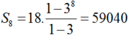

Chọn D
- Gọi u 1 , u 2 , . . . , u 7 là cấp số nhân cần tìm và q là công bội của cấp số nhân đó.
- Giả thiết ta có:
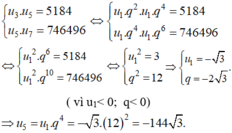

Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
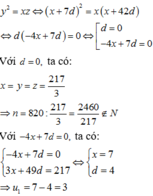
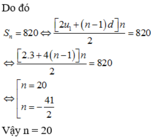

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
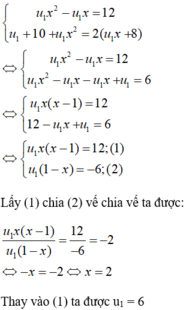
+ Tổng của năm số hạng đầu của CSN là:


De co cho thieu du kien la co bao nhieu so hang ko nhi ?Hay no la 1 csn lui vo han? Neu lui vo han thi lam duoc
\(\left\{{}\begin{matrix}q=4\\\dfrac{1}{u_1}+\dfrac{1}{u_2}+\dfrac{1}{u_3}+...+\dfrac{1}{u_n}+....=2\end{matrix}\right.\)
\(u_2=u_1.q;u_3=u_1.q^2;....;u_n=u_1.q^{n-1}\)
\(\Rightarrow\dfrac{1}{u_1}+\dfrac{1}{u_1.q}+\dfrac{1}{u_1.q^2}+...+\dfrac{1}{u_1.q^{n-1}}+....=2\)
\(\Leftrightarrow\dfrac{1}{u_1}\left(1+\dfrac{1}{q}+\dfrac{1}{q^2}+...+\dfrac{1}{q^{n-1}}+...\right)=2\)
Cần tính tổng trong ngoặc
\(\left\{{}\begin{matrix}u_1'=1\\q'=\dfrac{1}{q}\end{matrix}\right.\)
\(\Rightarrow S'_n=\dfrac{1}{1-q'}=\dfrac{1}{1-\dfrac{1}{4}}=\dfrac{4}{3}\)
\(\Rightarrow u_1=\dfrac{S'_n}{2}=\dfrac{4}{3.2}=\dfrac{2}{3}\)
Halo lau ko gap :)
\(\left\{{}\begin{matrix}u_1=\sqrt{2}\\u_2=u_1.q=-2\end{matrix}\right.\Rightarrow q=-\dfrac{2}{\sqrt{2}}=-\sqrt{2}\)
\(u_n=64\sqrt{2}=u_1.q^{n-1}\Leftrightarrow\sqrt{2}.\left(-\sqrt{2}\right)^{n-1}=64\sqrt{2}\)
\(\Leftrightarrow\left(-\sqrt{2}\right)^{n-1}=64\Rightarrow n-1=\log_{\sqrt{2}}64=12\Leftrightarrow n=13\)
\(S_{13}=u_1.\dfrac{q^{13}-1}{q-1}=\sqrt{2}.\dfrac{\left(-\sqrt{2}\right)^{13}-1}{-\sqrt{2}-1}=...\)
Check lại số má hộ tui nhó, số ghê quá
hélu@@@
bn giải sai hông nhở, tui k tìm thấy đáp án :33