cho tam giác ABC cân tại A.trên tia đối của tia BC lấy điểm D.trên tia đối của tia CB,lấy điểm E SAO CHO BD=CE.A)CM tam giác ABD=ACE .B)CM tam giác ADE cân tại A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
O
6 tháng 6 2023
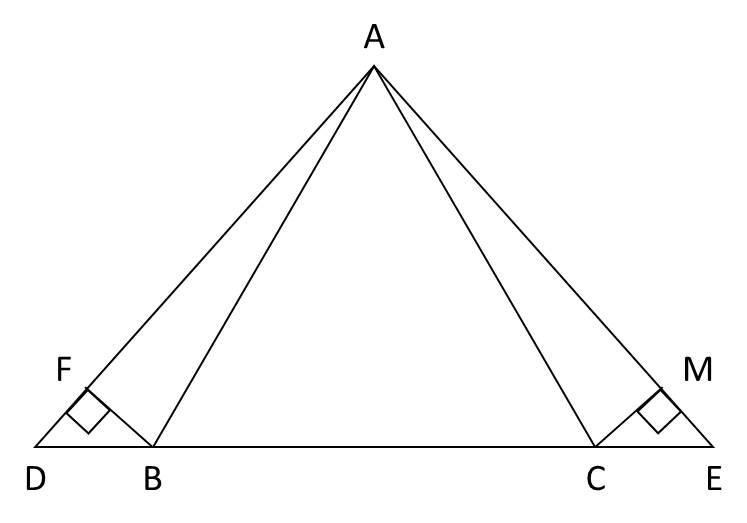
a, Vì tam giác ABC cân tại A
=> AB=AC, gócABC=gócACB
=> gócABD=gócACE
Xét tam giác ABD và tam giác ACE có
AB=AC, gócABD=gócACE, BD=CE
=> tam giác ABD = tam giác ACE (c-g-c)
=> gócCAE=gócBAD
b, Xét tam giác AMC và tam giác AFB có
gócAMC=gócAFB=90o, AC=AB, gócCAE=gócBAD
=> tam giác AMC = tam giác AFB (cạnh huyền góc nhọn)
=> AM=AF
=> tam giác AMF cân tại A
20 tháng 2 2021
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACE}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(Hai góc ở đáy của ΔBAC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE(gt)
\(\widehat{HDB}=\widehat{KEC}\)(ΔADB=ΔAEC)
Do đó: ΔHBD=ΔKCE(cạnh huyền-góc nhọn)
c) Ta có: ΔHBD=ΔKCE(cmt)
nên \(\widehat{HBD}=\widehat{KCE}\)(hai góc tương ứng)
mà \(\widehat{HBD}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCE}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định nghĩa tam giác cân)
D
11 tháng 1 2022
a, Ta có : ΔABC có AB = AC
⇒ ΔABC là tam giác cân
⇒ ∠B = ∠C = 180 - ∠A/2
Xét ΔADC và ΔAEB có :
DC = BE ( DB+BC = EC+CB )
∠ACD = ∠ABE ( chứng minh trên )
AC = AB
⇒ ΔADC = ΔAEB (c.g.c)
⇒ AD = AE ( 2 cạnh tương ứng )
b, Ta có : ∠ABD + ∠ABC = 180 ( 2 góc kề bù )
∠ACB + ∠ACE = 180 ( 2 góc kề bù )
Mà ∠ABC = ∠ACB
⇒ ∠ABD = ∠ACE
Xét ΔABD và ΔACE có :
AB = AD
∠ABD = ∠ACE
BD = CE
⇒ ΔABD = ΔACE (c.g.c)
11 tháng 1 2022
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
11 tháng 1 2022
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
26 tháng 4 2021
tam giác ABC cân tại A-->góc ABC=góc ACB (đ/lí tam giác cân)
góc ACE+góc ACB=180 độ (kề bù)
góc ABD+góc ABC=180 độ (kề bù)
mà góc ABC=góc ACB (cmt)
-->góc ACE=góc ABD (bắc cầu)
xét tam giác ABD và tam giác ACE có:
+AB=AC(gt)
+BD=CE(gt)
+góc ABD=góc ACE(cmt)
vậy tam giác ABD=tam giác ACE(cgc)
suy ra AD=AE
AD=AE(cmt)-->tam giác ADE cân tại A
26 tháng 4 2021
thank you!Thanks for ticking me! I didn't expect I was right, I also think you will tick later like everyone else! I didn't expect you to tick early>))
12 tháng 5 2023
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
b: ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
c: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
ΔADE cân tại A
mà AM vuông góc DE
nên AM là phân giác của góc DAE
d: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
=>ΔAHB=ΔAKC
=>AH=AK
=>ΔAHK cân tại A
7 tháng 2 2022
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
DO đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK và AH=AK
Xét ΔADE có
AH/AD=AK/AE
nên HK//DE
hay HK//BC
c: Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HBD}=\widehat{KCE}\)
Do đó: ΔHBD=ΔKCE
Suy ra: \(\widehat{HBD}=\widehat{KCE}\)
=>\(\widehat{OCB}=\widehat{OBC}\)
=>ΔOBC cân tại O
=>OB=OC
mà HB=CK
nên OB+HB=OC+CK
=>OH=OK
hay ΔOHK cân tại O
do tam giác ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{ABD}=\widehat{ACE}\) mà AB=AC và BD =CE
nên tam giác ABD =ACE theo th c.g.c
b. từ câu a ta có AD=AE nên tam giác ADE cân tại A