Cho hàm số \(y=\left(m-2\right)x+4+m\) . Tìm m để:a) Đồ thị hàm số đi qua điểm A (1 ; 2).b) Đồ thị hàm số cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 8 2023
a: Thay x=2 và y=9 vào (d), ta được:
2(m+4)+m-1=9
=>2m+8+m-1=9
=>3m=2
=>m=2/3
b: thay x=-1 và y=-7 vào (d), ta được:
-(m+4)+m-1=-7
=>-m-4+m-1=-7
=>-5=-7(vô lý)
TM
5 tháng 9 2023
1. Đồ thị của hàm số đi qua điểm \(M\left(2;3\right)\) nên giá trị hoành độ và tung độ của \(M\) là nghiệm của phương trình đường thẳng trên, tức:
\(3=m\cdot2+m-6\Leftrightarrow m=3\left(TM\right)\)
2. Đồ thị hàm số song song với đường thẳng \(\left(d\right):y=3x+2\), khi: \(\left\{{}\begin{matrix}m=3\\m-6\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne8\end{matrix}\right.\Rightarrow m=3\left(TM\right)\)
3. Gọi \(P\left(x_0;y_0\right)\) là điểm cố định mà đồ thị hàm số đi qua với mọi giá trị \(m\).
Khi đó: \(mx_0+m-6=y_0\Leftrightarrow\left(x_0+1\right)m-\left(y_0+6\right)=0\left(I\right)\)
Suy ra, phương trình \(\left(I\right)\) có vô số nghiệm, điều này xảy ra khi: \(\left\{{}\begin{matrix}x_0+1=0\\y_0+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-6\end{matrix}\right.\).
Vậy: Điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị \(m\) là \(P\left(-1;-6\right)\).
5 tháng 9 2023
1) \(y=mx+1\left(m\ne0\right)\left(1\right)\) hay \(mx-y+1=0\)
Để đồ thị hàm số \(\left(1\right)\) đi qua điểm \(M\left(-1;-1\right)\) khi và chỉ khi
\(m.\left(-1\right)+1=-1\)
\(\Leftrightarrow-m=-2\)
\(\Leftrightarrow m=2\)
Vậy hàm số \(\left(1\right):y=2x+1\)
Bạn tự vẽ đồ thị nhé!
2) \(y=\left(m^2-2\right)x+2m+3\left(d\right)\)
Để \(\left(1\right)//\left(d\right)\) khi và chỉ khi
\(\left\{{}\begin{matrix}m^2-2=2\\2m+3\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\2m\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\ne-1\end{matrix}\right.\) \(\Leftrightarrow m=\pm2\) thỏa đề bài
3) Khoảng cách từ gốc O đến đồ thị hàm số \(\left(1\right)\) là:
\(d\left(O;\left(1\right)\right)=\dfrac{m.0-0+1}{\sqrt[]{2^2+1^2}}=\dfrac{2}{\sqrt[]{5}}\)
\(\Leftrightarrow\dfrac{0.m+1}{\sqrt[]{5}}=\dfrac{2}{\sqrt[]{5}}\)
\(\Leftrightarrow0m=1\)
\(\Leftrightarrow m\in\varnothing\)
Vậy không có giá trị nào của m để thỏa mãn đề bài,
5 tháng 9 2023
Đáp án:
1. Tìm m để đồ thị hàm số (1) đi qua điểm M (−1;−1). Với m tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy
Để đồ thị hàm số (1) đi qua điểm M (−1;−1), ta cần có m(−1)+1=−1. Từ đó ta có m=−2.
Với m=−2, đồ thị hàm số (1) là một đường thẳng có hệ số góc -2 và đi qua điểm M (−1;−1). Ta có thể vẽ đồ thị hàm số như sau:
[Image of the graph of y=-2x+1]
2. Tìm giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 =
Hai đường thẳng song song khi hệ số góc của chúng bằng nhau. Do đó, ta có m=m2−2. Từ đó ta có m=2.
3. Tìm m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5
Khoảng cách từ gốc O đến đồ thị hàm số (1) là khoảng cách từ điểm (0;1) đến đường thẳng y=mx+1. Khoảng cách này được tính theo công thức:
d=|m|
Do đó, ta có d=2552=2.
Từ đó, ta có m=2.
Kết luận:
- Giá trị của m để đồ thị hàm số (1) đi qua điểm M (−1;−1) là m=-2.
- Giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 = là m=2.
- Giá trị của m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5 là m=2.
Lưu ý:
- Để giải bài toán 1 và 2, ta có thể thay m=-2 vào hàm số (1) và so sánh với tọa độ của điểm M (−1;−1) hoặc tọa độ của một điểm bất kỳ trên đường thẳng y (m² - 2) x + 2m+3 =.
- Để giải bài toán 3, ta có thể sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
chúc bạn học tốt
12 tháng 9 2023
a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
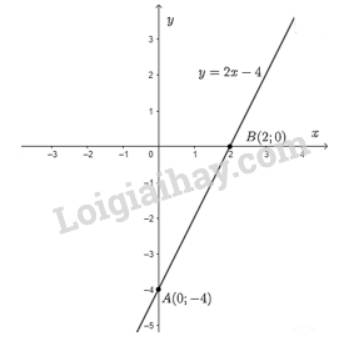
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
6 tháng 1 2021
a) Để hàm số trên đồng biến thì a>0 <=> m+5>0 <=> m>-5
b) thay A(2;3) vào đồ thị hs ta đc 3=(m+5).2+2m-10 =>m=3/4
27 tháng 10 2021
a: Thay x=1 và y=0 vào (d), ta được:
1-2m+3=0
\(\Leftrightarrow m=2\)
11 tháng 1
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-5-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
=>Đường thẳng \(y=\dfrac{m-5}{2}\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\)
Để đường tiệm cận ngang \(y=\dfrac{m-5}{2}\) đi qua M(-2;1) thì \(\dfrac{m-5}{2}=1\)
=>m-5=2
=>m=7
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
=>\(y=2m-1\) là đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
=>2m-1=1
=>2m=2
=>m=1
Để hàm số y=(m-2)x+4+m là hàm số bậc nhất thì \(m-2\ne0\)
hay \(m\ne2\)
a) Để đồ thị hàm số y=(m-2)x+4+m đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số y=(m-2)x+4+m, ta được
\(\left(m-2\right)\cdot1+4+m=2\)
\(\Leftrightarrow m-1+4+m=2\)
\(\Leftrightarrow2m+3=2\)
\(\Leftrightarrow2m=-1\)
hay \(m=-\dfrac{1}{2}\)(nhận)
Vậy: Để đồ thị hàm số y=(m-2)x+4+m đi qua điểm A(1;2) thì \(m=-\dfrac{1}{2}\)
Giúp mình ý b với