Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{AB}=\left(-1;-4\right)\)
Ta có: ABCD là hình bình hành
nên \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{DC}=\left(-1;-4\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D-3=-1\\y_D-3=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_D=2\\y_D=-1\end{matrix}\right.\)

\(\overrightarrow{CA}=\left(1-x_C;-2\right)\)
\(\overrightarrow{CB}=\left(-2-x_C;2\right)\)
\(\Leftrightarrow\left(x_C-1\right)\left(x_C+2\right)-4=0\)
\(\Leftrightarrow x_C^2+x_C-6=0\)
hay \(x_C=-3\)

a) Ta thấy \(\overrightarrow{AB}\left(3;2\right)\) và \(\overrightarrow{AC}\left(4;-3\right)\). Vì \(\dfrac{3}{4}\ne\dfrac{2}{-3}\) nên A, B, C không thẳng hàng.
b) Ta có \(\overrightarrow{BC}\left(1;-5\right)\)
Do vậy \(AB=\left|\overrightarrow{AB}\right|=\sqrt{3^2+2^2}=\sqrt{13}\)
\(AC=\left|\overrightarrow{AC}\right|=\sqrt{4^2+\left(-3\right)^2}=5\)
\(BC=\left|\overrightarrow{BC}\right|=\sqrt{1^2+\left(-5\right)^2}=\sqrt{26}\)
\(\Rightarrow C_{ABC}=AB+AC+BC=5+\sqrt{13}+\sqrt{26}\)
c) Gọi M, N, P lần lượt là trung điểm BC, CA, AB.
\(\Rightarrow P=\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\right)=\left(-\dfrac{3}{2};3\right)\)
\(N=\left(\dfrac{x_A+x_C}{2};\dfrac{y_A+y_C}{2}\right)=\left(-1;\dfrac{1}{2}\right)\)
\(M=\left(\dfrac{x_B+x_C}{2};\dfrac{y_B+y_C}{2}\right)=\left(\dfrac{1}{2};\dfrac{3}{2}\right)\)
d) Gọi G là trọng tâm tam giác ABC thì \(G=\left(\dfrac{x_A+x_B+x_C}{3};\dfrac{y_A+y_B+y_C}{3}\right)=\left(-\dfrac{2}{3};\dfrac{5}{3}\right)\)
e) Gọi \(D\left(x_D;y_D\right)\) là điểm thỏa mãn ycbt.
Để ABCD là hình bình hành thì \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\left(3;2\right)=\left(1-x_D;-1-y_D\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}3=1-x_D\\2=-1-y_D\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=-2\\y_D=-3\end{matrix}\right.\)
\(\Rightarrow D\left(-2;-3\right)\)
f) Bạn xem lại đề nhé.

Bài 1 :
Với x = 1 thì y = 4.1 = 4
Ta được \(A\left(1;4\right)\) thuộc đồ thị hàm số y = f(x) = 4x
Đường thẳng OA là đồ thị hàm số y = f(x) = 4x
y x 4 3 2 1 1 2 3 4 -1 -2 -3 -4 y=4x A
a) Ta có : \(f\left(2\right)=4\cdot2=8\)
\(f\left(-2\right)=4\cdot\left(-2\right)=-8\)
\(f\left(4\right)=4\cdot4=16\)
\(f\left(0\right)=4\cdot0=0\)
b) +) y = -1 thì \(4x=-1\) => \(x=-\frac{1}{4}\)
+) y = 0 thì 4x = 0 => x = 0
+) y = 2,5 thì 4x = 2,5 => \(4x=\frac{5}{2}\)=> x = \(\frac{5}{8}\)
Bài 2 :
a) Vẽ tương tự như bài 1
b) Thay \(M\left(-2,6\right)\)vào đths y = -3x ta có :
y =(-3)(-2) = 6
=> Điểm M thuộc đths y = -3x
c) Thay tung độ của P là 5 vào đồ thị hàm số y = -3x ta có :
=> 5 = -3x => \(x=-\frac{5}{3}\)
Vậy tọa độ của điểm P là \(P\left(-\frac{5}{3};5\right)\)

Tham khảo:
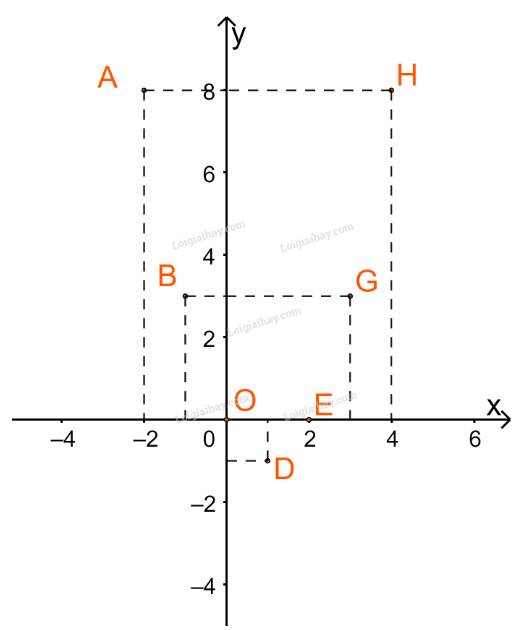
a) Tập xác định \(D = \{ - 2; - 1;0;1;2;3;4\} \)
b) Đồ thị gồm 7 điểm A (-2; 8), B (-1; 3), O (0; 0), D (1; -1), E (2; 0), G (3; 3), H (4; 8) như hình dưới

Tham khảo
a,⇒C,A,Da,⇒C,A,D thẳngthẳng hàng⇒−−→CA+−−→CD=→0⇔−−→CA=−−→DChàng⇒CA→+CD→=0→⇔CA→=DC→
D(x;y)⇒−−→CA=−−→DC⇔{−1−x=2−2−y=0D(x;y)⇒CA→=DC→⇔{−1−x=2−2−y=0⇔{x=−1y=−2⇔{x=−1y=−2⇔{x=−3y=−2⇔{x=−3y=−2⇒D(−3;−2)⇒D(−3;−2)
b,E(xo;yo)⇒−−→AE=−−→BCb,E(xo;yo)⇒AE→=BC→⇔{xo−1=−3yo+2=−5⇔{xo−1=−3yo+2=−5⇔{xo=−2yo=−7⇔{xo=−2yo=−7⇒E(−2;−7)⇒E(−2;−7)
c,⇒G(xG;yG)⇒⎧⎪ ⎪⎨⎪ ⎪⎩xG=1+2−13=23yG=−2+3−23=−13c,⇒G(xG;yG)⇒{xG=1+2−13=23yG=−2+3−23=−13⇒G(23;−13)
bạn ơi bạn có thể viết rõ câu trả lời hơn được không vì nó khó hiểu quá