Cho đường tròn (O), trên dây cung AB của đường tròn lấy các điểm E, F sao cho AE = EF = FB. Hỏi các góc AOE, EOF, FOE có bằng nhau hay không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

13 tháng 2 2017
hình( tự vẽ)
a) Chú ý: \(\widehat{AEB}=\widehat{AFB}=90\)(góc chắn nửa đường tròn) => H là trực tâm tam giác ABC
=> tứ giác AIFC nội tiếp (do \(\widehat{AIC}=\widehat{AFC}=90\)) => góc CIF= góc CAF
mà góc CAF=\(\frac{1}{2}\)góc EOF
mà EF=R => tam giác OEF đều => EOF =60 => CIF=30
b)
tam giác vuông AIC đồng dạng với tam giác vuông AEB (g-g)
=> AE.AC=AI.AB
Tương tự tam giác BIC đồng dạng BFA
=> BF.BC=BI.AB
Vậy: AE.AC+BF.BC=AB(AI+IB)=AB\(^2\)=4R\(^2\)=const (ĐPCM)


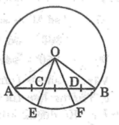

Giả sử các góc AOE, EOF, FOE bằng nhau.
Xét tam giác AOF, ta thấy OE vừa là đường trung tuyến, vừa là đường phân giác nên OE cũng là đường cao.
Suy ra OE \perp⊥ AB. (1)
Chứng minh tương tự, OF \perp⊥ AB. (2)
Từ (1) và (2) suy ra E \equiv≡ F (vô lý).
Vậy các góc AOE, EOF, FOE không bằng nhau.