cho đường tròn (O,R) từ điểm M nằm ngoài đường tròn kẻ tiếp tuyến MB,MC ; kẻ đường kính BD.chứng mibh BD//OM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Câu này đơn giản em tự giải.
b.
Ta có: \(\left\{{}\begin{matrix}OB=OC=R\\MB=MC\left(\text{t/c hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OM\) là trung trực của BC
\(\Rightarrow OM\perp BC\) tại H đồng thời H là trung điểm BC hay \(HB=HC\)
\(OC\perp MC\) (MC là tiếp tuyến tại C) \(\Rightarrow\Delta OMC\) vuông tại C
Áp dụng hệ thức lượng trong tam giác vuông OMC với đường cao CH:
\(CH^2=OH.MH\)
c.
C nằm trên đường tròn và AB là đường kính \(\Rightarrow\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\)
Xét hai tam giác MBH và BAC có:
\(\left\{{}\begin{matrix}\widehat{MHB}=\widehat{ACB}=90^0\\\widehat{MBH}=\widehat{BAC}\left(\text{cùng chắn BC}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBH\sim\Delta BAC\left(g.g\right)\)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{MH}{BC}\Rightarrow\dfrac{BH}{AC}=\dfrac{2HF}{2CH}\) (do F là trung điểm MH và H là trung điểm BC)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{HF}{CH}\)
Xét hai tam giác BHF và ACH có:
\(\left\{{}\begin{matrix}\dfrac{BH}{AC}=\dfrac{HF}{CH}\left(cmt\right)\\\widehat{BHF}=\widehat{ACH}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta BHF\sim\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{HBF}=\widehat{CAH}\)
Mà \(\widehat{CAH}=\widehat{CBQ}\) (cùng chắn CQ)
\(\Rightarrow\widehat{HBF}=\widehat{CBQ}\) hay \(\widehat{HBF}=\widehat{HBQ}\)
\(\Rightarrow B,Q,F\) thẳng hàng

Xét đường tròn tâm O ta có :
góc MAB = góc MCA = 1/2 sđ cung AB
Xét tam giác MAB và tam giác MCA có :
góc MAB = góc MCA
góc AMC Chung
=> \(\Delta MAB\sim\Delta MCA\)
=.> \(\dfrac{MA}{MC}=\dfrac{MB}{MA}\)
=> MA2=MC.MB
<=> 62=12.MB
=>MB =3cm
vậy MB = 3 cm

a) Xét tứ giác MAOB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: M,A,O,B cùng thuộc một đường tròn(đpcm)

Xét ΔMAD và ΔMCA có
góc MAD=góc MCA
góc AMD chung
=>ΔMAD đồng dạng với ΔMCA
=>MA/MC=MD/MA
=>MA^2=MC*MD

a: Xét tứ giác MBOC có \(\widehat{MBO}+\widehat{MCO}=90^0+90^0=180^0\)
=>MBOC là tứ giác nội tiếp
=>M,B,O,C cùng thuộc một đường tròn
b: Sửa đề: \(CH\cdot HB=OH\cdot HM\)
Xét (O) có
MB,MC là các tiếp tuyến
Do đó: MB=MC
=>M nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra MO là đường trung trực của BC
=>MO\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBM vuông tại B có BH là đường cao
nên \(OH\cdot HM=HB^2\)
=>\(OH\cdot HM=HB\cdot HC\)

a: Xét tứ giác MBOC có
\(\widehat{MBO}+\widehat{MCO}=180^0\)
Do đó: MBOC là tứ giác nội tiếp
Nhờ các mod xóa giùm bài kia. Gõ $\LaTeX$ bị sai.
Sửa đề. Chứng minh CD // OM.
Ta có:
$$\widehat{COM}=\dfrac{\widehat{BOC}}{2} =\dfrac{180^o-\widehat{DOC}}{2}=\widehat{OCD}$$
(vì $\Delta OCD$ cân tại $O$ do $OC=OD=R.$)
Nên CD//OM (hai góc so le trong bằng nhau)
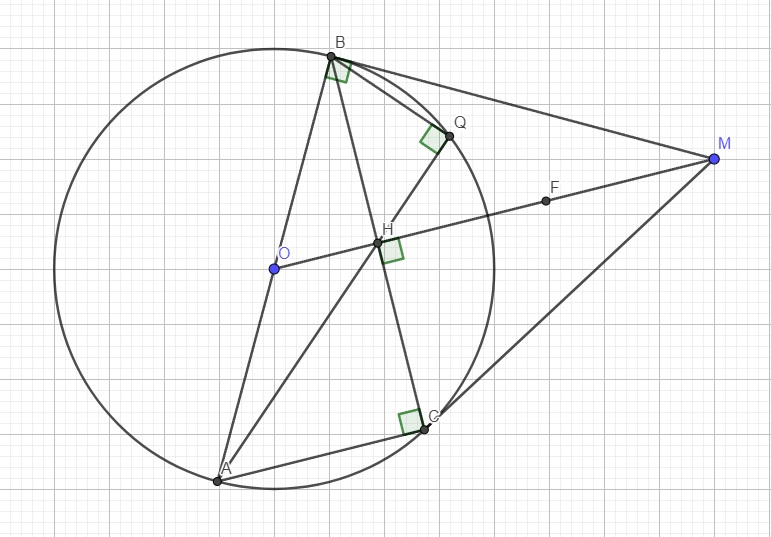
Hình vẽ: