Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có {BC⊥ABAB⊥SC⇒AB⊥CE{BC⊥ABAB⊥SC⇒AB⊥CE
Khi đó {CE⊥ABCE⊥SA⇒CE⊥(SAB){CE⊥ABCE⊥SA⇒CE⊥(SAB)
Áp dụng hệ thức lượng trong tam giác vuông ta có: SC2=SE.SB⇒SESB=SC2SB2SC2=SE.SB⇒SESB=SC2SB2, tương tự SDSE=SC2SA2SDSE=SC2SA2
Lại cả CA=AC√2=2a;VS.ABC=13SC.SABC=23a3CA=AC2=2a;VS.ABC=13SC.SABC=23a3
Khi đó VS.CDEVS.ABC=SESBSDSA=SC2SB2.SC2SA2=4648=13VS.CDEVS.ABC=SESBSDSA=SC2SB2.SC2SA2=4648=13
Do đó VS.CDE=13.23a3=2a39VS.CDE=13.23a3=2a39.

Đề bài thiếu bạn.
Đáy ABC chỉ biết 1 cạnh thì không thể xác định được các góc kia
Cần biết thêm 1 cạnh đáy nữa (ví dụ tam giác ABC vuông cân, hoặc cần thêm độ dài AB hay AC)

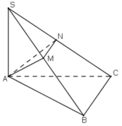
Gọi D là hình chiếu vuông góc của S lên (ABC)
\(SD\perp\left(ABC\right)\Rightarrow SD\perp AB\) , mà \(AB\perp SA\left(gt\right)\Rightarrow AB\perp\left(SAD\right)\Rightarrow AB\perp AD\)
\(\Rightarrow AD||BC\)
Tương tự ta có: \(BC\perp\left(SCD\right)\Rightarrow BC\perp CD\Rightarrow CD||AB\)
\(\Rightarrow\) Tứ giác ABCD là hình vuông
\(\Rightarrow BD=a\sqrt{2}\)
\(SD=\sqrt{SB^2-BD^2}=a\sqrt{2}\)
Gọi P là trung điểm AD \(\Rightarrow MP\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}MP=\dfrac{1}{2}SD=\dfrac{a\sqrt{2}}{2}\\MP||SD\Rightarrow MP\perp\left(ABC\right)\end{matrix}\right.\)
\(\Rightarrow\alpha=\widehat{MNP}\)
\(cos\alpha=\dfrac{NP}{MN}=\dfrac{NP}{\sqrt{NP^2+MP^2}}=\dfrac{a}{\sqrt{a^2+\dfrac{a^2}{2}}}=\dfrac{\sqrt{6}}{3}\)

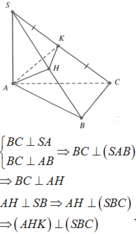
a: BC vuông góc SA
BC vuôg góc AB
=>BC vuông góc (SAB)
b: BI vuông góc SA
BI vuông góc AC
=>BI vuông góc (SAC)