Cho tam giác MNP vuông tại M , góc MNP =60 độ . Trên canh NP lấy D sao cho NM = ND . Từ D kẻ đường thẳng vuông góc vs NP cắt MP tại A a, CMR : NA là tia phân giác của góc MNP b, tam giác NMD là tam giác gì ? vì sao c, CMR : Tam giác NAP cân tại A và D là trung điểm NPd, Trên tia đối MN lấy B sao cho MB = DP . CMR : tam giác APB cân tại A e, CMR : D,A,B thẳng hàngf, CMR : MD //...
Đọc tiếp
Cho tam giác MNP vuông tại M , góc MNP =60 độ . Trên canh NP lấy D sao cho NM = ND . Từ D kẻ đường thẳng vuông góc vs NP cắt MP tại A
a, CMR : NA là tia phân giác của góc MNP
b, tam giác NMD là tam giác gì ? vì sao
c, CMR : Tam giác NAP cân tại A và D là trung điểm NP
d, Trên tia đối MN lấy B sao cho MB = DP . CMR : tam giác APB cân tại A
e, CMR : D,A,B thẳng hàng
f, CMR : MD // BP
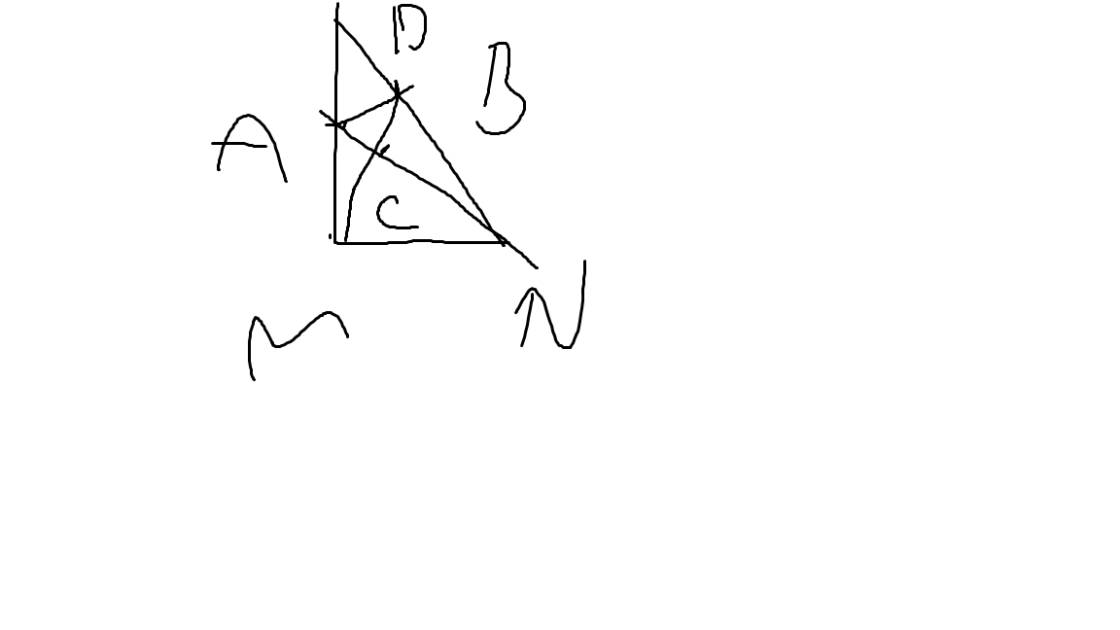
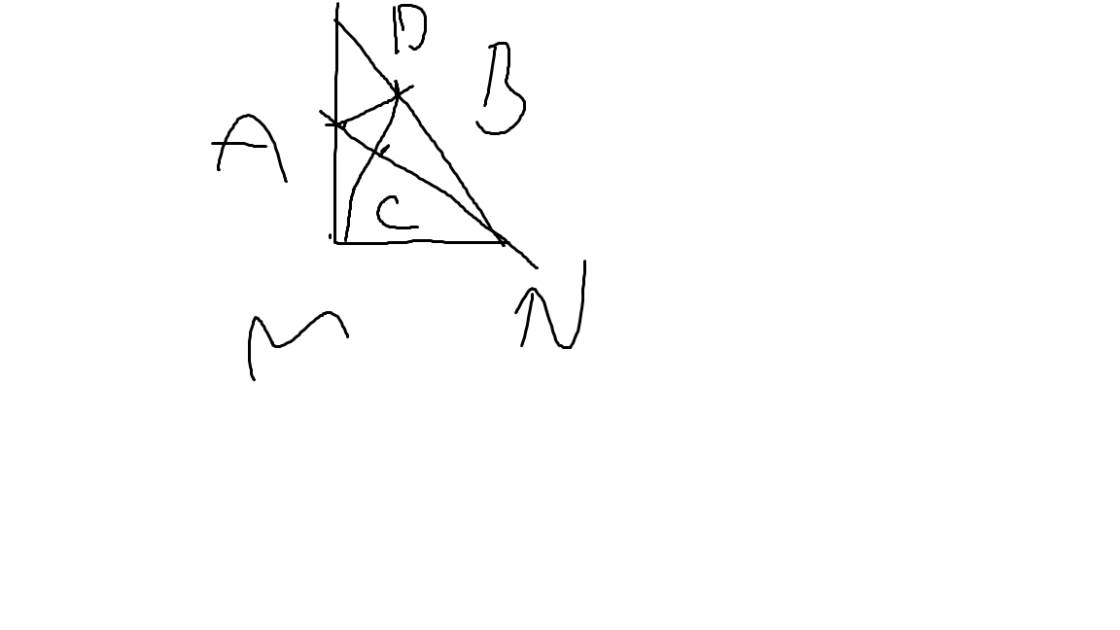
a) Xét ΔNAM vuông tại M và ΔNDA vuông tại D có
NA chung
NA=ND(gt)
Do đó: ΔNAM=ΔNDA(cạnh huyền-cạnh góc vuông)
⇒\(\widehat{MNA}=\widehat{DNA}\)(hai góc tương ứng)
mà tia NA nằm giữa hai tia NM,NDnên NA là tia phân giác của \(\widehat{NMD}\)hay NA là tia phan giác của \(\widehat{NMP}\)(đpcm)b) Xét ΔNMD có NM=ND(gt)nên ΔNMD cân tại N(Định nghĩa tam giác cân)Xét ΔNMD cân tại N có \(\widehat{MND}=60^0\)(gt)nên ΔNMD đều(Dấu hiệu nhận biết tam giác đều)c) Ta có: ΔNMP vuông tại M(gt)nên \(\widehat{NMP}+\widehat{MPN}=90^0\)(hai góc nhọn phụ nhau)\(\Leftrightarrow\widehat{MPN}=90^0-\widehat{NMP}=90^0-60^0=30^0\)(1)Ta có: NA là tia phân giác của \(\widehat{MNP}\)(cmt)nên \(\widehat{PNA}=\dfrac{\widehat{MNP}}{2}=\dfrac{60^0}{2}=30^0\)(2)Từ (1) và (2) suy ra \(\widehat{APN}=\widehat{ANP}\)Xét ΔANP có \(\widehat{APN}=\widehat{ANP}\)(cmt)nên ΔANP cân tại A(Định lí đảo của tam giác cân)Ta có: ΔANP cân tại A(gt)mà AD là đường cao ứng với cạnh đáy NP(gt)nên AD là đường trung tuyến ứng với cạnh NP(Định lí tam giác cân)hay D là trung điểm của NP(đpcm)