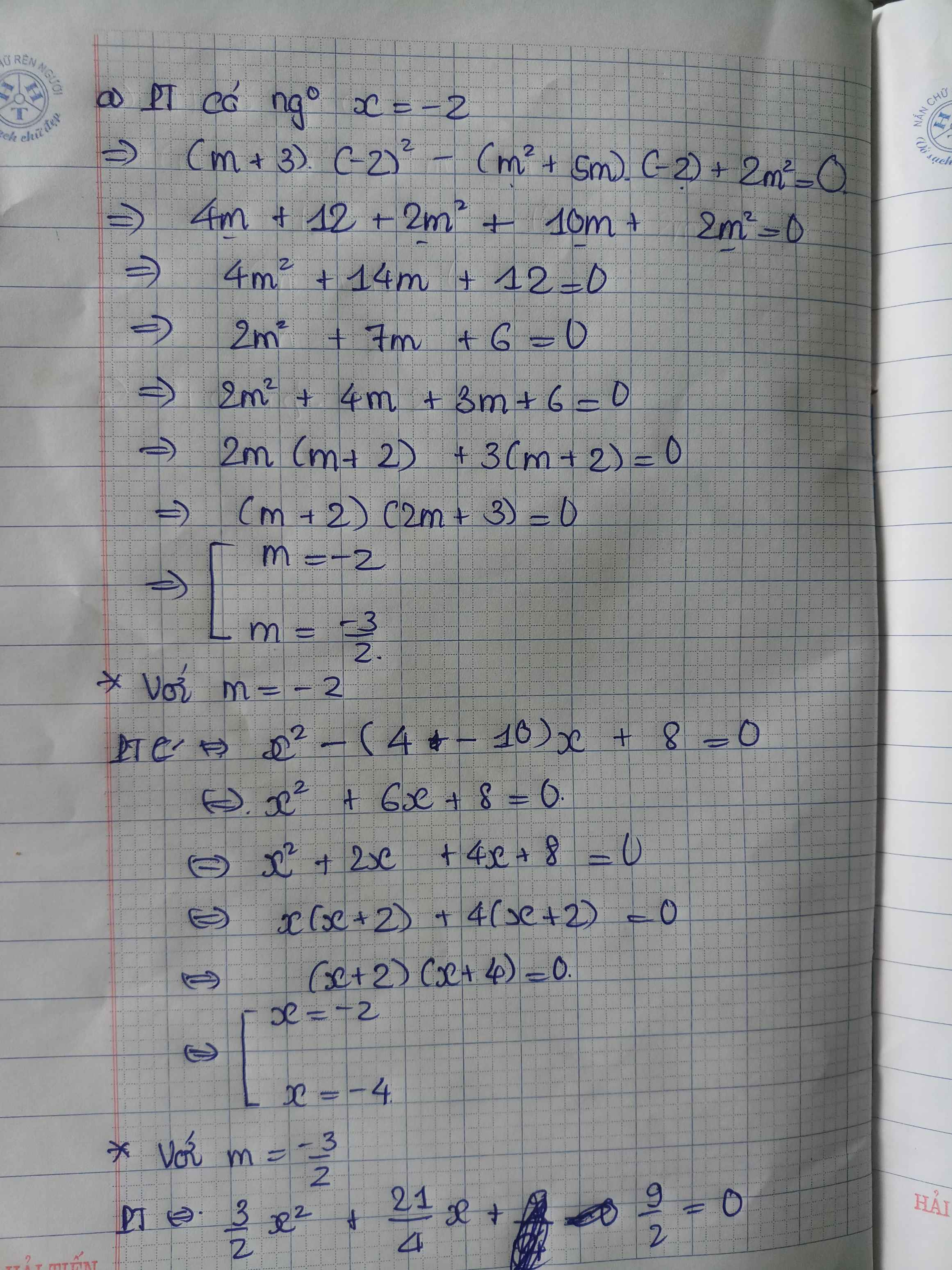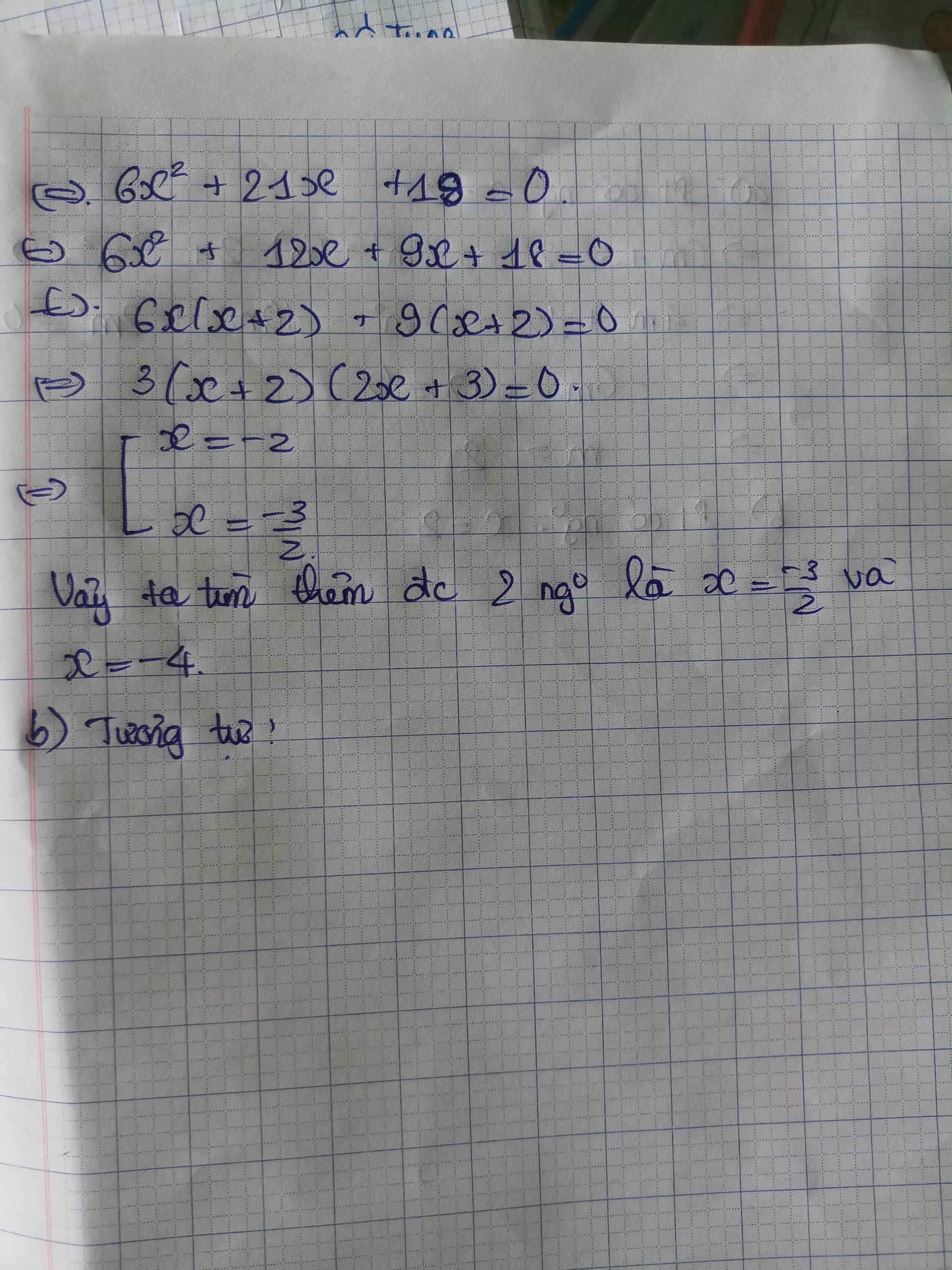Tìm a để phương trình \(\left(a-1\right)x^3-\left(a^2-a+2\right)x^2+\left(a-1\right)x+a^2+a=0\)có 3 nghiệm phân biệt T a unit of weight equivalent to 1000 kilograms More (Definitions, Synonyms, Translation)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 4 2021
a, Thay m vào pt ta được :
(3+1).x2-2(3+1).x+3-3=0
\(\Leftrightarrow\)4x2-8x=0
\(\Leftrightarrow4x\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy m=3 phương trình có 2 nghiệm là 0 và 2
b, Theo Vi et ta có :
\(\left\{{}\begin{matrix}x_1.x_2=\dfrac{m-3}{m+1}\\x_1+x_2=\dfrac{2\left(m+1\right)}{m+1}\end{matrix}\right.\left(vớim\ne-1\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1.x_2=\dfrac{m-3}{m+1}\\x_1+x_2=2\end{matrix}\right.\) (1)
Ta có : (4x1+1)(4x2+1)=18
\(\Leftrightarrow16x_1.x_2+4x_1+4x_2+1=18\)
\(\Leftrightarrow16.x_1.x_2+4\left(x_1+x_2\right)=17\) (2)
Thay (1) vào (2) ta được :
16.\(\dfrac{m-3}{m+1}+4.2=17\)
\(\Leftrightarrow\dfrac{16m-48}{m+1}=9\)
\(\Leftrightarrow9\left(m+1\right)=16m-48\)
\(\Leftrightarrow9m+9=16m-48\)
\(\Leftrightarrow7m=57\)
\(\Leftrightarrow m=\dfrac{57}{7}\) (thỏa mãn m\(\ne-1\))
Vậy ..
H
3 tháng 4 2021
a. Khi m=2 thì (1) có dạng :
\(x^2-6\left(2-1\right)x+9\left(2-3\right)=0\\ \Leftrightarrow x^2-6x-9=0\\ \Leftrightarrow\left(x-3\right)^2=18\Leftrightarrow x-3=\pm\sqrt{18}\\ \Leftrightarrow x=3\pm3\sqrt{2}\)
Vậy với m=2 thì tập nghiệm của phương trình là \(S=\left\{3\pm3\sqrt{2}\right\}\)
b. Coi (1) là phương trình bậc 2 ẩn x , ta có:
\(\text{Δ}'=\left(-3m+3\right)^2-1\cdot9\left(m-3\right)=9m^2-18m+9-9m+27\\ =9m^2-27m+36=\left(3m-\dfrac{9}{2}\right)^2+\dfrac{63}{4}>0\)
Nên phương trình (1) luôn có 2 nghiệm x1,x2 thỏa mãn:
\(\left\{{}\begin{matrix}x_1+x_2=6\left(m-1\right)\\x_1x_2=9\left(m-3\right)\end{matrix}\right.\left(2\right)\)
Vì
\(x_1+x_2=2x_1x_2\\ \Leftrightarrow6\left(m-1\right)=18\left(m-3\right)\Leftrightarrow m-1=3m-9\\ \Leftrightarrow2m=8\Leftrightarrow m=4\)
Vậy m=4
3 tháng 4 2021
b) Ta có: \(\text{Δ}=\left[-6\left(m-1\right)\right]^2-4\cdot1\cdot9\left(m-3\right)\)
\(=\left(6m-6\right)^2-36\left(m-3\right)\)
\(=36m^2-72m+36-36m+108\)
\(=36m^2-108m+144\)
\(=\left(6m\right)^2-2\cdot6m\cdot9+81+63\)
\(=\left(6m-9\right)^2+63>0\forall m\)
Suy ra: Phương trình luôn có hai nghiệm phân biệt với mọi m
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=6\left(m-1\right)=6m-6\\x_1\cdot x_2=9\left(m-3\right)=9m-27\end{matrix}\right.\)
Ta có: \(x_1+x_2=2x_1\cdot x_2\)
\(\Leftrightarrow6m-6=2\left(9m-27\right)\)
\(\Leftrightarrow6m-6-18m+54=0\)
\(\Leftrightarrow-12m+48=0\)
\(\Leftrightarrow-12m=-48\)
hay m=4
Vậy: m=4
18 tháng 4 2023
1:
\(=\left(\dfrac{1}{x-2\sqrt{x}}+\dfrac{2}{3\sqrt{x}-6}\right):\dfrac{2\sqrt{x}+3}{3\sqrt{x}}\)
\(=\dfrac{3+2\sqrt{x}}{3\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{3\sqrt{x}}{2\sqrt{x}+3}=\dfrac{1}{\sqrt{x}-2}\)
30 tháng 7 2021
b) Thay x=2 vào pt, ta được:
\(4\left(m^2-1\right)-4m+m^2+m+4=0\)
\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)
\(\Leftrightarrow5m^2-3m=0\)
\(\Leftrightarrow m\left(5m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=\dfrac{2m}{m^2-1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
Pt đã cho có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(2m+9\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\-m^2-5m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\-5< m< 0\end{matrix}\right.\)
\(\Rightarrow m=\left\{-4;-3;-2\right\}\) có 3 giá trị nguyên
19 tháng 5 2020
a) PT có nghiệm kép nếu
\(\hept{\begin{cases}m-1\ne0\\\Delta'=\left(m-1\right)^2+m\left(m-1\right)=0\end{cases}\Leftrightarrow\hept{\begin{cases}m\ne1\\\left(m-1\right)\left(2m-1\right)=0\end{cases}\Leftrightarrow}m=\frac{1}{2}}\)
Vậy \(m=\frac{1}{2}\)thì pt có nghiệm kép
\(x_1=x_2=-\frac{b}{2a}=-\frac{2\left(m-1\right)}{2\left(m-1\right)}=-1\)
b) Để pt có nghiệm phân biệt đều âm thì
\(\hept{\begin{cases}m-1\ne0\\\Delta'=\left(m-1\right)\left(2m-1\right)>0\end{cases}}\)
\(\hept{\begin{cases}x_1\cdot x_2=-\frac{m}{m-1}>0\\x_1+x_2=\frac{2\left(m-1\right)}{m-1}< 0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}m>1\\m< \frac{1}{2}\end{cases}}\)và \(0< m< 1\)
Vậy 0<m<\(\frac{1}{2}\)
PN
19 tháng 5 2020
định gõ ấn f5 cái thì thấy bạn làm xong r :((
giải nhanh quá !
5 tháng 1 2022
a: \(\Leftrightarrow\left(2m+1\right)^2-4\left(m^2-3\right)=0\)
\(\Leftrightarrow4m^2+4m+1-4m^2+12=0\)
=>4m=-13
hay m=-13/4
c: \(\Leftrightarrow\left(2m-2\right)^2-4m^2>=0\)
\(\Leftrightarrow4m^2-8m+4-4m^2>=0\)
=>-8m>=-4
hay m<=1/2