Đèn Đ ghi: 6V-6W, R1=3 ôm, Đ nt R1, Uab không đổi a/ tính điện trở của đèn và điện trở của mạch AB b/ Biết đèn sáng bình thường. Tính hiệu điện thế của R1 và nhiệt lượng tỏa ra trên mạch AB trong 5'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 10 2021
\(\left(R1//R2\right)ntRd\Rightarrow\left\{{}\begin{matrix}Id=Idm=I12=2\Rightarrow U12=I12.\left(\dfrac{R1R2}{R1+R2}\right)=3,75V\\\Rightarrow Um=Udm+U12=6+3,75=9,75V\\I1=\dfrac{U12}{R1}=\dfrac{3,75}{5}=0,75A\\I2=Im-I1=2-0,75=1,25A\end{matrix}\right.\)
N
1 tháng 11 2021
a. \(R=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=2+\left(\dfrac{6.3}{6+3}\right)=4\left(\Omega\right)\)
b. \(I=I1=I23=\dfrac{U}{R}=\dfrac{12}{4}=3A\left(R1ntR23\right)\)
\(U23=U2=U3=I13.R23=3\left(\dfrac{6.3}{6+3}\right)=6\left(V\right)\)(R2//R3)
\(\left\{{}\begin{matrix}I2=U2:R2=6:6=1A\\I3=U3:R3=6:3=2A\end{matrix}\right.\)
c. \(U_d=U_{23}=6V\Rightarrow\) đèn sáng bình thường.
Q
13 tháng 6 2021
a, khi chỉnh con chạy C RAC=24 => RBC=12
lúc này mạch điện vẽ lại (R1//RAC)nt(RCB//Rđ)
\(R_đ=\dfrac{6^2}{6}=6\left(\Omega\right)\)
\(R_{tđ}=\dfrac{R_1.R_{AC}}{R_1+R_{AC}}+\dfrac{R_{CB}.R_đ}{R_{CB}+R_đ}=12\left(\Omega\right)\)
\(I=\dfrac{10,8}{12}=0,9\left(A\right)\)
\(\Rightarrow U_{đCB}=I.R_{đCB}=0,9.4=3,6\left(V\right)\)
\(\Rightarrow I_đ=\dfrac{3,6}{6}=0,6\left(A\right)\)
mà cđ dđ định mức của đèn là 6/6=1(A)
ta thấy \(I_đ< 1\) nên đèn sáng yếu hơn bình thường
b, vị trí đèn sáng bth \(R_{AC}=x\Rightarrow R_{CB}=36-x\)
khi đó \(I_đ=1\) \(\Rightarrow U_{BC}=6\Rightarrow I_{BC}=\dfrac{6}{36-x}\)
\(\Rightarrow I=\dfrac{6}{36-x}+1\left(1\right)\)
\(\Rightarrow U_{1AC}=10,8-6=4,8\left(V\right)\)
\(\Rightarrow I=\dfrac{4,8.\left(12+x\right)}{12x}\left(2\right)\)
từ (1) (2) \(\Rightarrow x=6\left(\Omega\right)\)
\(\Rightarrow\dfrac{R_{AC}}{R_{CB}}=\dfrac{6}{30}=\dfrac{1}{5}\)
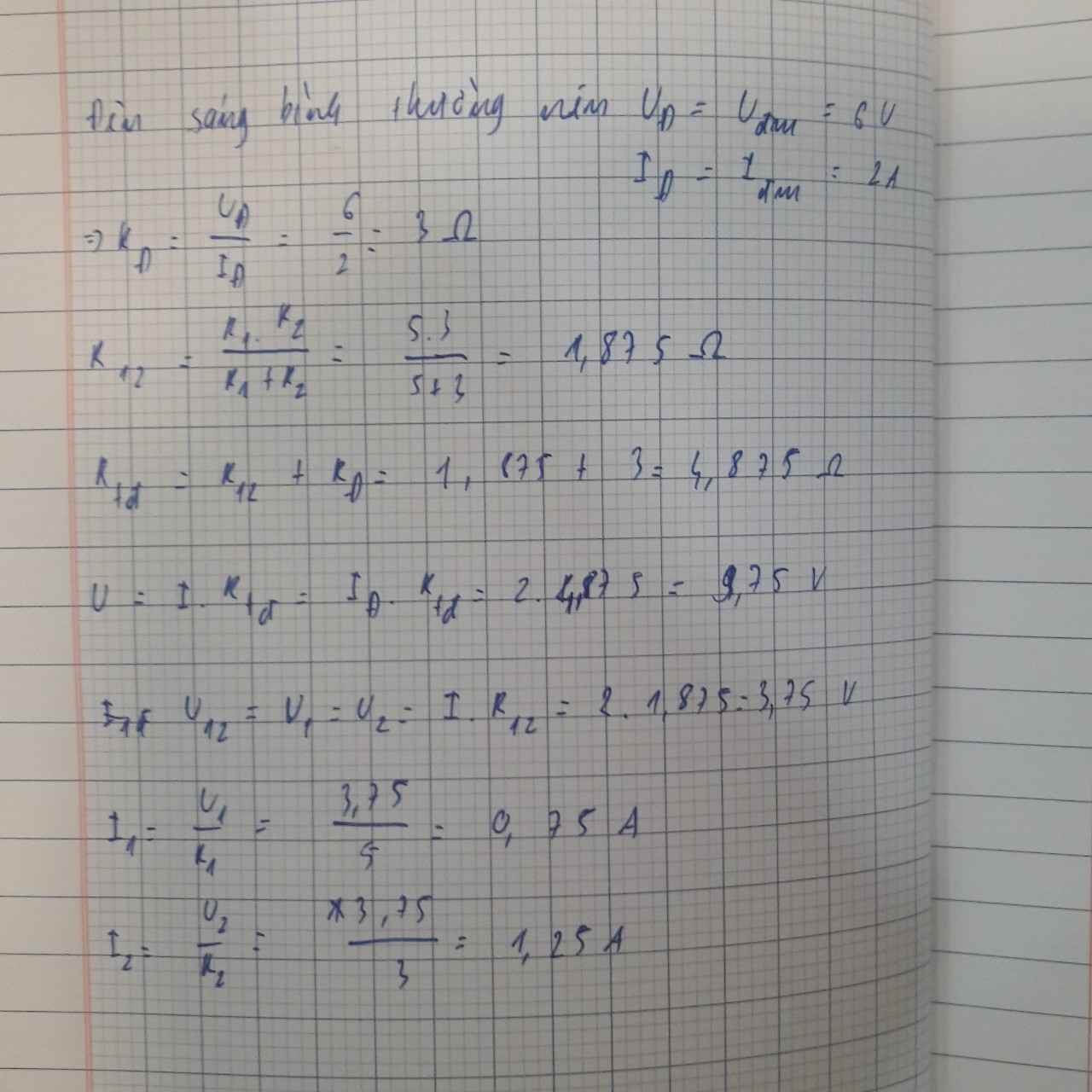
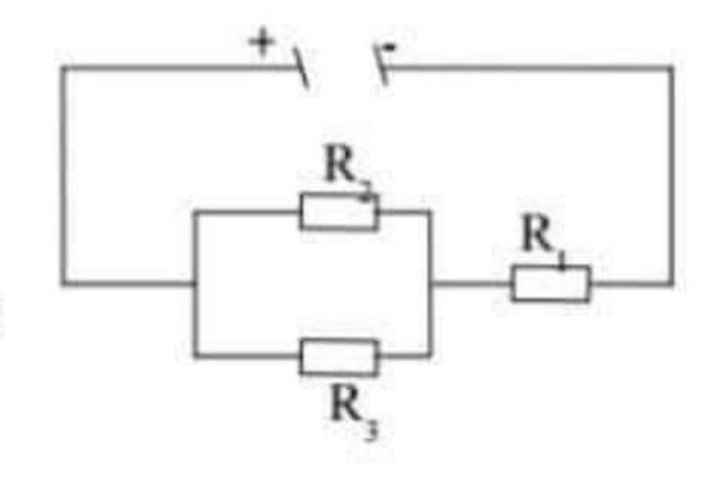
\(R_D=\dfrac{U_{dm}^2}{P_{dm}}=\dfrac{36}{6}=6\left(\Omega\right)\)
\(R_DntR_1\Rightarrow R_{td}=R_1+R_D=3+6=9\left(\Omega\right)\)
\(I=I_{dm}=\dfrac{P_{dm}}{U_{dm}}=\dfrac{6}{6}=1\left(A\right)\)
\(\Rightarrow U_1=I.R_1=1.3=3\left(V\right)\)
\(Q=I^2.R_{td}.t=1.9.5.60=2700\left(J\right)\)