Cho hình vuông ABCD cạnh a, tâm O
Tìm quỹ tích điểm M thỏa mãn
MA2 + MB2 + MC2 = 3MD2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
0
CM
23 tháng 2 2017
Đáp án D
Với tứ diện đều ABCD thì mặt cầu (S) là mặt cầu có tâm trùng với tâm của mặt cầu ngoại tiếp tứ diện ABCD và là trọng tâm của tứ diện đều cạnh a, đồng thời có bán kính R = a 2 4
Gọi G là trọng tâm của tứ diện ⇒ G A ¯ + G B ¯ + G C ¯ + G D ¯ = 0 ¯
Ta có:
T = M A 2 + M B 2 + M C 2 + M D 2 = M G ¯ + G A ¯ 2 + M G ¯ + G B ¯ 2 + M G ¯ + G C ¯ 2 + M G ¯ + G D ¯ 2
= 4 M G 2 + 2 M G ¯ G A ¯ + G B ¯ + G C ¯ + G D ¯ ⏟ 0 + G A 2 + G B 2 + G C 2 + G D 2 = 4 M G 2 + 4 G A 2
= 4 a 2 4 2 + 4 a 6 4 2 = 2 a 2 . Vậy T = M A 2 + M B 2 + M C 2 + M D 2 = 2 a 2
CM
8 tháng 9 2017
Đáp án C.
Gắn hệ trục tọa độ Oxyz, với O(0;0;0) là trung điểm của AB => OC= 3
Khi đó
⇒ x 2 + ( y + 1 ) 2 + z 2 + x 2 + ( y - 1 ) 2 + z 2 + 2 ( x - 3 ) 2 + 2 y 2 + 2 z 2 = 12
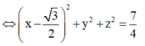
Vậy tập hợp các điểm M là một mặt cầu có bán kính
R
=
7
2
Gọi O là tâm hình vuông \(\Rightarrow OA=OB=OC=OD\)
\(\left(\overrightarrow{MO}+\overrightarrow{OA}\right)^2+\left(\overrightarrow{MO}+\overrightarrow{OB}\right)^2+\left(\overrightarrow{MO}+\overrightarrow{OC}\right)^2=3\left(\overrightarrow{MO}+\overrightarrow{OD}\right)^2\)
\(\Leftrightarrow OA^2+OB^2+OC^2+2\overrightarrow{MO}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)=3OD^2+6\overrightarrow{MO}.\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{MO}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-3\overrightarrow{OD}\right)=0\)
\(\Leftrightarrow\overrightarrow{MO}\left(\overrightarrow{OB}-3\overrightarrow{OD}\right)=0\)
\(\Leftrightarrow\overrightarrow{MO}.\overrightarrow{OB}=0\)
Quỹ tích M là đường thẳng AC