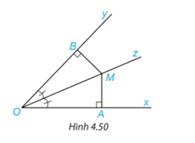
Cho xOy ̂ , trên tia phân giác của góc đó lấy một điểm M, kẻ MA, MB vuông góc lần lượt với Ox, Oy. Chứng minh rằng: a) ΔMAB cân; b) AB ⊥ OM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
NH
12 tháng 4 2020
a, Xét △OAM vuông tại A và △OBM vuông tại B
Có: AOM = BOM (gt)
OM là cạnh chung
=> △OAM = △OBM (ch-gn)
=> AM = BM (2 cạnh tương ứng)
và OA = OB (2 cạnh tương ứng)
=> △OAB cân tại O
b, Xét △MAD vuông tại A và △MBE vuông tại B
Có: AM = MB (cmt)
AMD = BME (2 góc đối đỉnh)
=> △MAD = △MBE (cgv-gnk)
=> MD = ME (2 cạnh tương ứng)
c, Gọi OM ∩ DE = { I }
Ta có: OA + AD = OD và OB + BE = OE
Mà OA = OB (cmt) , AD = BE (△MAD = △MBE)
=> OD = OE
Xét △IOD và △IOE
Có: OD = OE (cmt)
DOI = EOI (gt)
OI là cạnh chung
=> △IOD = △IOE (c.g.c)
=> OID = OIE (2 góc tương ứng)
Mà OID + OIE = 180o (2 góc kề bù)
=> OID = OIE = 180o : 2 = 90o
=> OI ⊥ DE
Mà OM ∩ DE = { I }
=> OM ⊥ DE
24 tháng 4 2020
a) Xét \(\Delta OMH\)và \(\Delta OMK\)có :
OM chung
\(\widehat{O_1}=\widehat{O_2}\)( do Oz là tia phân giác của ^xOy )
=> \(\Delta OMH=\Delta OMK\)( cạnh huyền - góc nhọn )
=> \(MH=MK\)( hai cạnh tương ứng )
b) Từ \(\Delta OMH=\Delta OMK\)=> \(OH=OK\)( hai cạnh tương ứng )
Xét \(\Delta MBK\)và \(\Delta MAH\)có :
\(MB=MA\)( gt )
\(MH=MK\)( cmt )
=> \(\Delta MBK=\Delta MAH\)( cạnh huyền - cạnh góc vuông )
=> \(BK=AH\)( hai cạnh tương ứng )
Ta có : \(OH=OA+AH\)
\(OK=OB+BK\)
mà OH = OK ; AH = BK
=> OA = OB ( đpcm )
24 tháng 4 2020
Bạn kiểm tra lại đề từ chỗ M là điểm bất kì nằm trên Ox đến hểt
BA
6 tháng 12 2015
a) Xét tam giác vuông AMO và tam giác vuông BMO :
góc MOA = góc MOB (gt)
OM là cạnh chung
=>tam giác vuông AMO = tam giác vuông BMO (cạnh huyền + góc nhọn)
=> OA=OB ( 2 cạnh tương ứng)
b) theo a) ta có : tam giác AMO = tam giác BMO
=>góc AMO = góc BMO
=> MO là tia phân giác của góc AMB
c) gọi C là giao điểm của OM và AB
Xét tam giác OAC và tam giác OBC có:
góc AOC = góc BOC (gt)
OC là cạnh chung
OA = OB (theo a)
=>tam giác OAC = tam giác OBC
=> góc ACO = góc BCO
mà hai góc này kề bù
=> góc ACO = góc BCO = 90 độ
=> OM vuông góc với AB
22 tháng 1
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
=>MA=MB
Xét ΔMAF vuông tại A và ΔMBE vuông tại B có
MA=MB
\(\widehat{AMF}=\widehat{BME}\)
Do đó: ΔMAF=ΔMBE
=>MF=ME
b:
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(1)
Ta có: MA=MB
=>M nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra OM là đường trung trực của BA
=>OM\(\perp\)BA