Tìm tập hợp các gtri của m để đt y=-1 cắt đồ thị hàm số : \(y=x^4-\left(3m+2\right)x^2+3m\) tại 4 điểm pb có hoành độ nhỏ hơn 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình hoành độ giao điểm của \(\left(C_m\right)\) và đường thẳng y = -1 là :
\(x^4-\left(3m+2\right)x^2+3m=-1\Leftrightarrow\left(x^2-1\right)\left(x^2-3m-1\right)=0\)
Đường thẳng y = -1 cắt \(\left(C_m\right)\) tại 4 điểm phân biệt có hoành độ nhỏ hơn 2 khi và chỉ khi :
\(0 < 3m+1 < 4\) và \(3m+1\ne1\)
\(\Leftrightarrow\)\(-\frac{1}{3}< m\)< 1 và \(m\ne0\)

Câu 2:
Thay x=0 và y=-3 vào (d), ta được:
m+2=-3
hay m=-5

a. Đồ thị cắt trục hoành tại điểm có hoành độ bằng 2
=> x = 2 và y = 0
=> 0 = (2 + 3m ) .2 + 4
<=> 2 + 3m = -2 <=> m = -4/3
b. Đồ thị cắt trục tung tại điểm có tug độ bằng 4 => x = 0 và y = 4
=> 4 = ( 2 + 3m) .0 + 4
<=> 4 = 4 luôn đúng với mọi m
Vậy mọi m thì đồ thị cắt trục tug tại điểm có tung độ bằng 4

(d) cắt trục hoành độ là 1:
⇒ \(x=1\)
Và hàm số: \(y=0\)
Thay \(x=1\) tại giá trị hàm số \(y=0\)
Ta có:
\(y=\left(m-3\right)\cdot1+3m-1=0\)
\(\Leftrightarrow\left(m-3\right)+3m-1=0\)
\(\Leftrightarrow m-3+3m-1=0\)
\(\Leftrightarrow4m-4=0\)
\(\Leftrightarrow4m=4\)
\(\Leftrightarrow m=1\)
Vậy: ...
3: Thay x=1 và y=0 vào (d), ta được:
m-3+3m-1=0
=>4m-4=0
=>m=1

Lời giải:
PT hoành độ giao điểm:
$(m-3)x+3m-1=2x+10$
$\Leftrightarrow (m-5)x+3m-11=0(*)$
Để 2 đt cắt nhau tại điểm có hoành độ $12$ thì PT $(*)$ có nghiệm $x=12$
$\Leftrightarrow (m-5).12+3m-11=0$
$\Leftrightarrow m=\frac{71}{15}$

Ta có : \(y'=3x^2-2\left(m-1\right)x+3m+1\)
Gọi \(M\left(x_0;y_0\right)\) là tiếp điểm, ta có : \(x_0=1\Rightarrow y_0=3m+1,y'\left(1\right)=m+6\)
Phương trình tiếp tuyến tại M : \(y=\left(m+6\right)\left(x-1\right)+3m+1\)
Tiếp tuyến đi qua A \(\Leftrightarrow-1=m+6+3m+1\Leftrightarrow m=-2\)
Vậy m = -2 là giá trị cần tìm


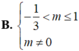
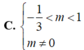


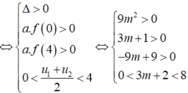


phương trình hoành độ giao điểm của f(x) với y = -1 là
x4 - (3m + 2)x2 + 3m = -1
⇔ x4 - (3m + 2)x2 + 3m + 1 = 0 (1)
Đặt x2 = t (ĐK : t ≥ 0)
Phương trình trở thành
t2 - (3m + 2)t + 3m + 1 = 0 (2)
Để (1) có 4 nghiệm phân biệt nhỏ hơn 2 thì (2) có 2 nghiệm phân biệt thỏa mãn 0 < t < 4
⇒ \(\left\{{}\begin{matrix}9-9m< 0\\3m+1>0\end{matrix}\right.\) (cái này bạn vẽ bảng biến thiên ra là xong)
⇒ \(\dfrac{-1}{3}< m< 1\)
Vậy tập hợp giá trị m cần tìm là \(\left(\dfrac{-1}{3};1\right)\)
Hình như 0 k lấy