Cho tam giác ABC vuông tại A.Trên nửa mặt phẳng bờ BC có chứa A,kẻ tia Cx// AB.Trên tia Cx lấy D sao cho CD=AB.O là trung ddiểm AC .lấy M trên AD và N trên BC sao cho AM=CN.Chứng minh M,O,N thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

7 tháng 9 2021
a: Xét tứ giác ABDC có
M là trung điểm của đường chéo AD
M là trung điểm của đường chéo BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD và AB=CD

28 tháng 8 2021
a: Xét tứ giác ABDC có
M là trung điểm của đường chéo AD
M là trung điểm của đường chéo BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD và AB=CD

31 tháng 8 2019
Đề gì vậy
ngay phân a đã có M là trung điểm AD rồi
giờ câu b lại chứng minh M là trung điểm AD
??? đề viết kiểu gì vậy
2 tháng 9 2019
LƯU Ý : Phần a và phần b là 2 bài khác nhau , 2 phần ấy không liên quan gì đến nhau cả , mỗi phần là 1 bài làm khác nhau nhé mọi người <33

17 tháng 12 2021
2: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
Suy ra: AD//BC
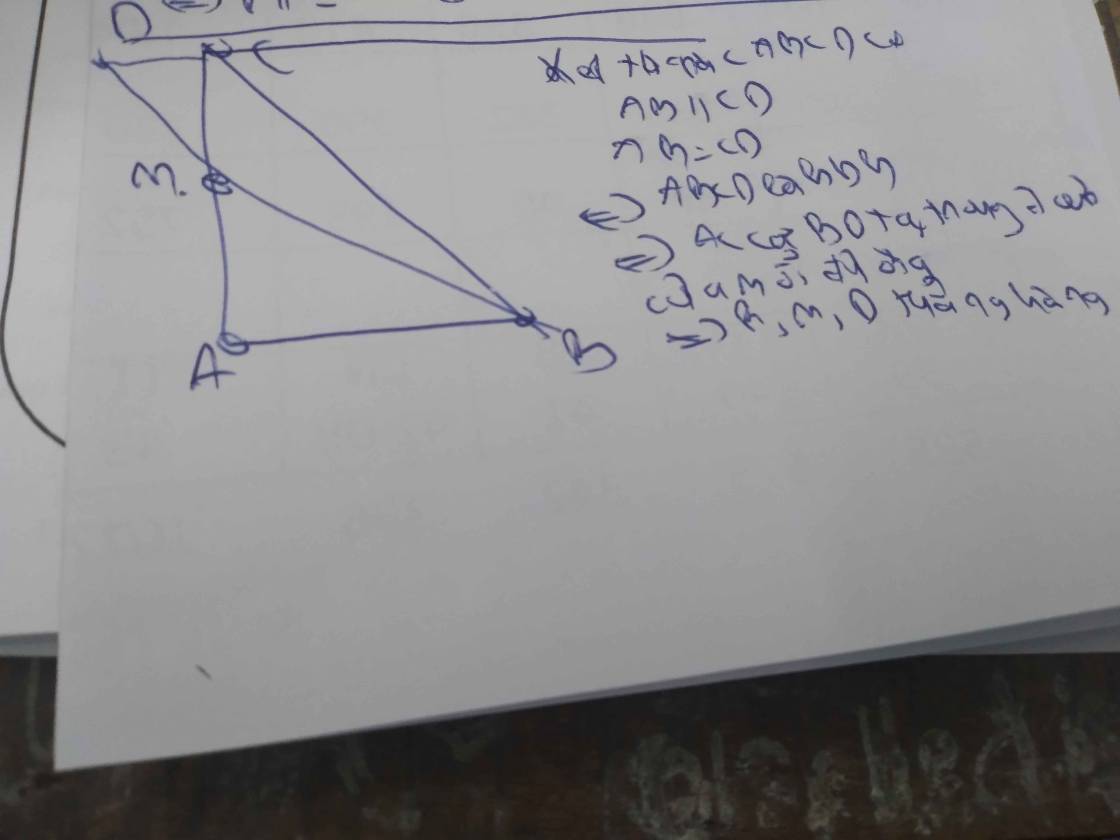

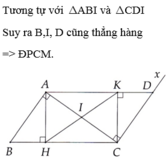
Nay không có điện thoại nên đánh máy hơi lâu :VV
Xét \(\Delta ABC\) và \(\Delta CDA:\)
AB=CD(gt)
AC: cạnh chung
\(\widehat{BAC}=\widehat{DCA}=90^o\)
-> \(\Delta ABC=\Delta CDA\left(c.g.c\right)\)
->\(\widehat{BCA}=\widehat{DAC}\)(2 góc t/ứ)
Xét \(\Delta AOM\) và \(\Delta CON:\)
OA=OC(gt)
\(AM=CN\left(gt\right)\) (2 góc đối đỉnh)
\(\widehat{OAM}=\widehat{OCN}\left(cmt\right)\)
->\(\Delta AOM=\Delta CON\left(c.g.c\right)\)
->\(\widehat{MOA}=\widehat{NOC}\)(2 góc t/ứ)
Lại có: \(\widehat{MOA}+\widehat{MOC}=180^o\) (2 góc kề bù)
-> \(\widehat{NOC}+\widehat{MOC}=180^o\)
-> \(\widehat{NOM}=180^o\)
-> N,O, M thẳng hàng