1Cho tam giác MNP có N=90,MN =4 cm, NP =7 cm. Tính BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề: MN-NP=3cm
ΔABC=ΔMNP
=>AB=MN; BC=NP; AC=MP
MN-NP=3
=>AB-BC=3
mà AB+BC=7
nên \(AB=\dfrac{3+7}{2}=5cm;BC=AB-3=5-3=2cm\)
MP=AC
mà MP=4cm
nên AC=4cm
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=5+4+2=11\left(cm\right)\)
Chu vi tam giác MNP là:
\(C_{MNP}=MN+NP+MP=5+4+2=11\left(cm\right)\)

a, Vì \(NP^2=46,24=10,24+36=MN^2+MP^2\) nên tg MNP vuông tại M
b, Áp dụng HTL: \(\left\{{}\begin{matrix}KN=\dfrac{MN^2}{NP}=\dfrac{128}{85}\left(cm\right)\\KP=\dfrac{MP^2}{NP}=\dfrac{90}{17}\left(cm\right)\\MK=\sqrt{KN\cdot NP}=\dfrac{48}{17}\left(cm\right)\end{matrix}\right.\)
c, \(S_{MNP}=\dfrac{1}{2}MN\cdot MP=\dfrac{1}{2}\cdot6\cdot3,2=9,6\left(cm^2\right)\)

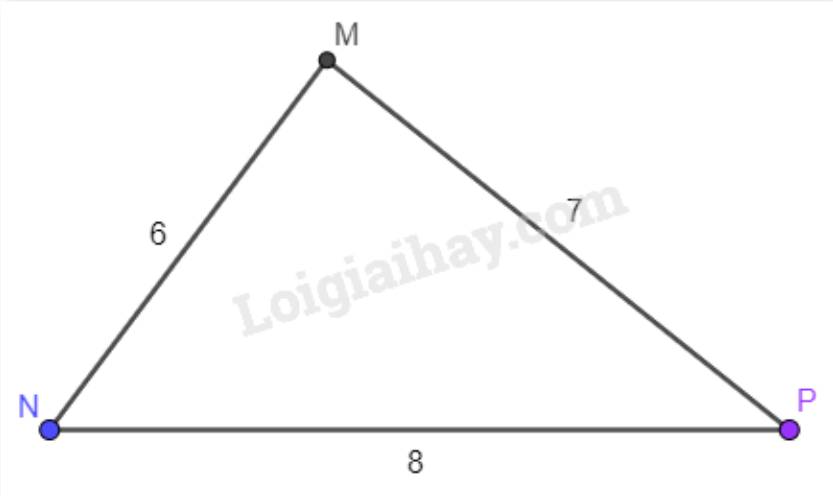
Trong tam giác MNP ta có: \(MN < MP < NP\) (6 < 7 < 8).
Vậy góc lớn nhất trong tam giác MNP là góc M (đối diện với cạnh NP) và góc nhỏ nhất trong tam giác MNP là góc P (đối diện với cạnh MN).

Bước 1: Vẽ NP = 7cm
Bước 2: Tại điểm N vẽ cung tròn tâm N bán kính MN = 4cm
Tại điểm P vẽ cung tròn tâm P bán kính MP = 5cm
2 cung tròn này cắt nhau ở đâu thì đó là điểm M
Bước 3: Nối MN, MP ta được tam giác MNP
Cứ làm theo 3 bước trên ta vẽ được tam giác MNP

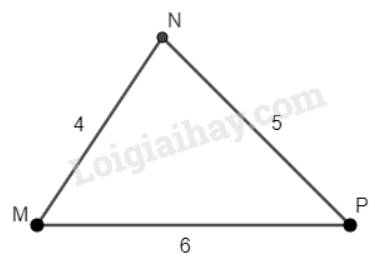
Trong tam giác MNP: \(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)

ta có MN=cosN x NP=0,766 x 5=3,83
Vì góc N phụ với góc P
góc P=M-N=90-30=60

Áp dụng định lý Pitago:
\(MP^2=MN^2+NP^2 \\ \Leftrightarrow MP^2=4^2+7^2 \\ \Rightarrow MP= \sqrt{65} (cm)\)
Vậy \(MP=\sqrt{65} cm\).