tìm m để y=\(\dfrac{cos2x+msin2x+1}{cos2x+2}\) đặt giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 8 2021
\(y^2=sin2x+cos2x+2\sqrt{sin2x.cos2x}\)
Đặt \(sin2x+cos2x=t\Rightarrow t\in\left[1;\dfrac{1+\sqrt{3}}{2}\right]\)
\(sin2x.cos2x=\dfrac{t^2-1}{2}\)
\(y^2=f\left(t\right)=t+\sqrt{2\left(t^2-1\right)}\)
\(f'\left(t\right)=1+\dfrac{2t}{\sqrt{2\left(t^2-1\right)}}>0\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow y^2\le f\left(\dfrac{1+\sqrt{3}}{2}\right)=\dfrac{\left(1+\sqrt[4]{3}\right)^2}{2}\)
\(\Rightarrow y\le\dfrac{1+\sqrt[4]{3}}{\sqrt{2}}\)
CM
23 tháng 5 2017
Đáp án D
Ta có: y = 2 1 2 sin 2 x - 1 2 cos 2 x = 2 sin 2 x - π 4 ≤ 2 . 1 = 2 ⇔ sin 2 x - π 4 ⇔ 2 x - π 4 = π 2 + k 2 π ⇔ x = 3 π 8 + kπ
Vậy M = 2 .
PT
1
MQ
0
PT
1
CM
4 tháng 1 2018
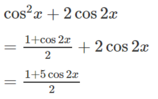
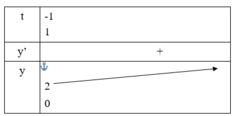
Vì -1 ≤ cos2x ≤ 1 nên giá trị lớn nhất của y là 3, đạt được khi x = 0, giá trị nhỏ nhất của y là -2, đạt được khi x = π/2
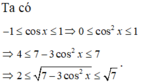
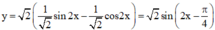
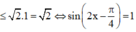
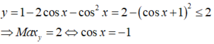
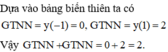
\(y.cos2x+2y=cos2x+m.sin2x+1\)
\(\Leftrightarrow m.sin2x+\left(1-y\right)cos2x=2y-1\)
\(\Rightarrow m^2+\left(1-y\right)^2\ge\left(2y-1\right)^2\)
\(\Rightarrow3y^2-2y-m^2\le0\)
\(\Rightarrow\dfrac{1-\sqrt{1+3m^2}}{3}\le y\le\dfrac{1+\sqrt{1+3m^2}}{3}\)
Bạn coi lại đề, m càng lớn thì max y càng lớn. Câu hỏi chính xác của đề bài là gì?