1. Cho 3 số lập thành cấp số cộng. Biết tổng 3 số bằng 6 và tổng bình phương 3 số bằng 30. Tìm các số.
2. Tìm m để phương trình sau có 4 nghiệm lập thành cấp số cộng:
\(x^4-10x^2+9m=0\)
3. Cho cấp số cộng giảm thỏa mãn:
\(\left\{{}\begin{matrix}u_1+u_2+u_3=3\\u_3^2-u_2^2=3\end{matrix}\right.\)
Tính: \(S=\dfrac{1}{u_1u_2}+\dfrac{1}{u_2u_3}+...+\dfrac{1}{u_{19}u_{20}}\)
4. Cho cấp số cộng tăng:
\(\left\{{}\begin{matrix}u_1+u_3+u_5=-3\\u_2+u_4+u_6=3\end{matrix}\right.\)
Tính: \(S=u_1+u_4+u_7+...+u_{88}\)
Mọi người giúp mình với ạ!!! Mình cảm ơn mọi người nhiều!!!

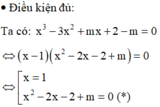
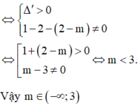
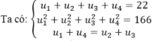
Câu 1: Gọi 3 số là a;b;c
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=6\\2b=a+c\\a^2+b^2+c^2=30\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\a+c=4\\a^2+c^2=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}b=2\\c=4-a\\a^2+\left(4-a\right)^2=26\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=2\\c=5\\a=-1\end{matrix}\right.\left(\text{V\text{ì} }a< c\right)\)
Câu 2: Đặt \(t=x^2\left(t\ge0\right)\)
\(pt:x^4-10\text{x}^2+9m=0\left(1\right)\\ \Leftrightarrow t^2-10t^2+9m=0\left(2\right)\)
Để pt(1) có 4 nghiệm lập thành cấp số cộng thì (2) phải có 2 nghiệm dương phân biệt
\(\)\(\Rightarrow\left\{{}\begin{matrix}\Delta'=\left(-5\right)^2-9m>0\\S=10>0\left(T/m\right)\\P=9m>0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m< \dfrac{25}{9}\\\\m>0\end{matrix}\right.\\ \Rightarrow0< m< \dfrac{25}{9}\)
(2) có 2 nghiệm \(t_1< t_2\)
=> (1) có 4 nghiệm \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
\(\Rightarrow\sqrt{t_1}=\sqrt{t_2}-\sqrt{t_1}\\ \Rightarrow4t_1=t_2\\ \Rightarrow\left\{{}\begin{matrix}t_1+t_2=10\\4t_1=t_2\\t_1t_2=9m\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}t_1=2\\t_2=8\\m=\dfrac{16}{9}\left(t/m\right)\end{matrix}\right.\)