
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



F1: tròn : dài = 3 :1
=> tròn trội hoàn toàn so với dài
Quy ước : A: tròn ; a :dài
=> P : Aa (tròn ) x Aa (Tròn)
G A ,a A, a
F1: 1AA :2Aa :1 aa
TLKH : 3 tròn : 1 dài
b) Tự thụ phấn
sdl1: AA x AA
G A A
F2: AA (100% tròn)
sdl2: Aa x Aa
G A, a A,a
F2: 1AA :2Aa :1aa
TLKH : 3 tròn : 1 dài
sdl3: aa x aa
G a a
F2: aa (100% dài)


a: 3x+21=57
=>3x=57-21
=>3x=36
=>\(x=\dfrac{36}{3}=12\)
b: \(2x-138=2^3\cdot3^2\)
=>\(2x-138=8\cdot9=72\)
=>2x=72+138=210
=>x=105
c: \(4x^3+12=120\)
=>\(4x^3=120-12=108\)
=>\(x^3=27=3^3\)
=>x=3
\(a)3x+21=57\\ \Leftrightarrow3x=57-21\\ \Leftrightarrow3x=36\\ \Leftrightarrow x=\dfrac{36}{3}\\ \Leftrightarrow x=12\\ b)2x-138=2^3\cdot3^2\\ \Leftrightarrow2x-138=72\\ \Leftrightarrow2x=72+138\\ \Leftrightarrow2x=210\\ \Leftrightarrow x=\dfrac{210}{2}\\ \Leftrightarrow x=105\\ c)4x^3+12=120\\ \Leftrightarrow4x^3=120-12\\ \Leftrightarrow4x^3=108\\ \Leftrightarrow x^3=\dfrac{108}{4}\\ \Leftrightarrow x^3=27\\ \Leftrightarrow x^3=3^3\\ \Leftrightarrow x=3.\)










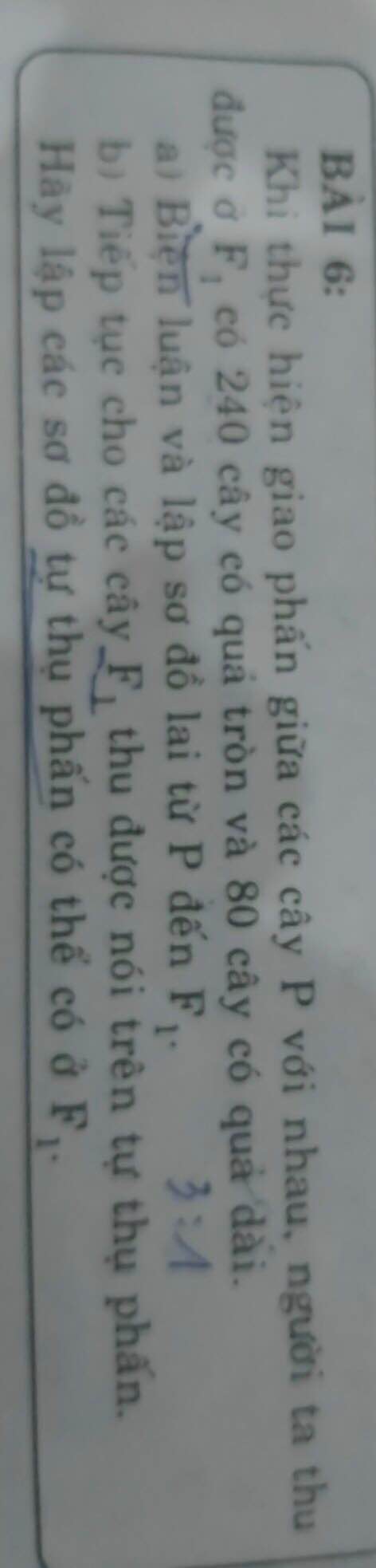
 dễ nhìn hơn nha mn
dễ nhìn hơn nha mn

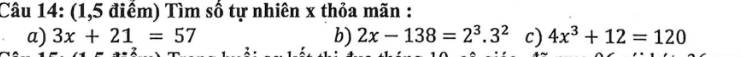 giúp tớ vs ạ. thanks
giúp tớ vs ạ. thanks
a, Điều kiện xác định của A là : \(\hept{\begin{cases}3x-6\ne0\\x^2-2x\ne0\end{cases}\Rightarrow\hept{\begin{cases}3\left(x-2\right)\ne0\\x\left(x-2\right)\ne0\end{cases}\Rightarrow x\ne}0;2}\)
Vậy \(x\ne0;2\)
b, \(A=\frac{x}{3x-6}+\frac{2x+3}{x^2-2x}\)
\(=\frac{x}{3\left(x-2\right)}+\frac{2x+3}{x\left(x-2\right)}=\frac{x^2}{3x\left(x-2\right)}+\frac{6x+9}{3x\left(x-2\right)}=\frac{x^2+6x+9}{3x\left(x-2\right)}\)
c, Ta có : A = 0 hay
\(\frac{x^2+6x+9}{3x\left(x-2\right)}=0\Leftrightarrow\left(x+3\right)^2=0\Leftrightarrow x=-3\)
Vậy x = -3 thì A = 0