Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AC//BE

a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC

a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
b: Ta có: ΔMAB=ΔMEC
=>AB=EC
Ta có: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
c: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BE
d: Xét ΔIAM và ΔKEM có
IA=KE
\(\widehat{IAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔIAM=ΔKEM
=>\(\widehat{IMA}=\widehat{KME}\)
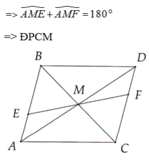
mà \(\widehat{IMA}+\widehat{IME}=180^0\)(hai góc kề bù)
nên \(\widehat{KME}+\widehat{IME}=180^0\)
=>I,M,K thẳng hàng

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC và AB=EC
c: Xét ΔBCD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔBCD cân tại C
d: Xét ΔOBC có
OM là đường cao
OM là đường trung tuyến
Do đó: ΔOBC cân tại O
Suy ra: OB=OC(1)
Xét ΔOBD có
OA là đường cao
OA là đường trung tuyến
Do đó: ΔOBD cân tại O
Suy ra: OB=OD(2)
Từ (1) và (2) suy ra OB=OC=OD
hay O cách đều ba đỉnh của ΔBDC

vẽ hình ; bạn tự vẽ nha
a) Xét tam giác MAB và tam giác MEC
có AM =ME
BM=MC
góc AMB=gócBME
vạy tam giác MAB=tam giác MEC.(c.g.c)
b) vì tam giác AMC=tam giác MEC
=> góc EAC= góc EAC
=>AC//BE
c) Tam giác AMB=tam giác CME=>gócABC = gócBCE
=>Tam giác IMB =tam giác CMK(c.g.c)
=>góc IMB= góc CMK
T/C BMI+IMC=180
=>góc CMK +IMC=180
=>IMK=180
Vậy I,M,K thẳng hàng

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: BA=DC; AC=DB
Xét ΔBAC và ΔCDB có
BA=CD
AC=DB
BC chung
Do đó: ΔBAC=ΔCDB
c: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó: AEDF là hình bình hành
Suy ra: AD và FE cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AD
nên M là trung điểm của FE
hay F,M,E thẳng hàng

Xét ABM và EMC có : AM = ME BM = CM Góc AMB = góc CME ( đối đỉnh ) => tam giac ABM = Tam giác EMC Ta có : Tam giác AMB = tam giác EMC nên góc BAM = góc EMC Mặt khác : 2 góc BAM và AEC nắm vị trí so le trong => AB // CE c Xét tam giác AIB và tam gics CIK có : AI = IC BI = Ik Góc AIB = góc CIK ( đối đỉnh ) => tam giác AIB = tam giác CIK