Một gói hàng trọng lượng 400N trượt trên một sơi dây nilon. Sức căng cực đại mà dây chịu đc khi gói hàng trượt xuống 250N, Gia tốc tối thiểu mà gói hàng p trượt trên sợi dây là
A. 5,37 m/s2
B. 3,75m/s2
C. 3,57 m/s2
D. 5,73m/s2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 4 2022
Công thực hiện:
\(A=Fs\cdot cos\alpha=250\cdot10\cdot cos45^o=1768N\)
Chọn B
13 tháng 12 2023
a) Biểu diễn lực căng dây:
Lực căng dây là lực mà dây kéo lên gói hàng để duy trì nó ở vị trí cao. Theo nguyên lý Newton thứ ba, lực căng dây có cùng độ lớn nhưng ngược chiều với lực trọng trên gói hàng. Vì vậy, lực căng dây có độ lớn là 150N và hướng lực là ngược chiều với hướng lực trọng.
b) Lực tác dụng của cậu bé:
Để giữ gói hàng đứng yên trên cao, cậu bé phải tạo ra một lực tác dụng lên gói hàng có độ lớn bằng đúng lực trọng của gói hàng. Vì vậy, lực tác dụng của cậu bé cần có độ lớn là 150N và hướng lực cần phải trùng với hướng lực trọng.
VT
25 tháng 12 2017
C
Sợi dây treo bị đứt và quả cầu rơi xuống đất. Đó là do lực căng lớn nhất mà dây chịu được nhỏ hơn trọng lượng của vật là p = 10m = 0,5.10 = 5N.
VT
9 tháng 8 2018
Sợi dây treo bị đứt và quả cầu rơi xuống đất. Đó là lực căng lớn nhất mà dây chịu được nhỏ hơn trọng lượng của vật là P = 10.m = 0,5.10 = 5 N
⇒ Đáp án C
31 tháng 3 2023
Chọn hệ trục tọa độ Oxy như hình vẽ. Gọi \(\overrightarrow{F_k}\) là lực kéo tác dụng lên sợi dây, \(\overrightarrow{P}\) và \(\overrightarrow{N}\) lần lượt là trọng lực tác dụng lên vật. Ta phân tích \(\overrightarrow{F_k}\) thành 2 lực \(\overrightarrow{F_{k_x}}\) và \(\overrightarrow{F_{k_y}}\) trên các trục Ox, Oy.
a) Công của lực kéo là \(A_k=F_k.s.cos\left(\overrightarrow{F_k},\overrightarrow{s}\right)=100.20.cos45^o=1000\sqrt{2}\left(J\right)\)
b) Gọi \(\overrightarrow{F_{ms}}\) là lực ma sát tác dụng lên vật. Chọn chiều dương là chiều chuyển động của vật
Áp dụng định luật II Newton:
\(\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\) (1)
Chiếu (1) lên Oy: \(N=P-F_{k_y}=400-F_k.sin45^o=400-175\sqrt{2}\left(N\right)\)
Do đề bài không nói gì về loại chuyển động của vật nên mình sẽ xem đây là chuyển động nhanh dần đều nhé. Khi đó, ta sẽ có \(s=\dfrac{1}{2}at^2\Rightarrow20=\dfrac{1}{2}a.180^2\) \(\Rightarrow a=\dfrac{1}{810}\left(m/s^2\right)\).
Chiếu (1) lên Ox, ta được \(F_{k_x}-F_{ms}=m.a\Rightarrow F_{ms}=F_{k_x}-m.a=350.cos45^o-400.\dfrac{1}{180}\)\(=170\sqrt{2}-\dfrac{20}{9}\) (N)
\(\Rightarrow A_{ms}=-\left(170\sqrt{2}-\dfrac{20}{9}\right).20\approx-4763,88\left(J\right)\)
26 tháng 3 2022
Công kéo vật:
\(A=F\cdot s\cdot cos\alpha=150\cdot15\cdot cos45^o=1590,99J\)
Công suất thực hiện:
\(P=\dfrac{A}{t}=F\cdot v=150\cdot1,5=225W\)
VT
23 tháng 9 2017
Đáp án B
+ Có ba lực tác dụng lên vật khi vật trượt xuống mặt phẳng nghiêng:
Gồm trọng lực P ⇀ được phân tích thành hai thành phần Px→ và Py→ ; lực ma sát Fms→ ; phản lực N ⇀ .
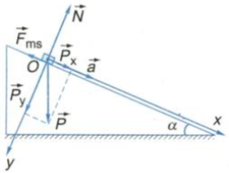
+ Áp dụng định luật II Niuton, ta
có: P ⇀ + F m s ⇀ + N ⇀ = m.a→ (1)
+ Chọn hệ trục gồm: Ox hướng theo chiều chuyển động của vật: trên mặt phẳng nghiêng, Oy vuông góc với Ox và hướng xuống.
+ Chiếu biểu thức vecto (1) lên trục Ox, Oy ta được:
Theo trục Ox: Px – Fms = ma
⟺ Px – μ .N = ma (2)
Theo trục Oy: Py - N = 0 (3) (theo trục Oy vật không có gia tốc)
Thế (3) vào (2):
a = P x − μ . P y m = m g sin α − μ m g . cos α m = g ( sin α − μ . cos α )
Kết quả cho thấy gia tốc a của vật trượt có ma sát trên mặt phẳng nghiêng phụ thuộc vào g , μ , α
VT
26 tháng 6 2018
Đáp án B
+ Có ba lực tác dụng lên vật khi vật trượt xuống mặt phẳng nghiêng:
Gồm trọng lực P → được phân tích thành hai thành phần P → x ; P → y lực ma sát F m s → ; phản lực N → .
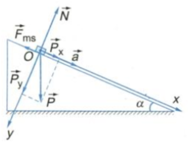
+ Áp dụng định luật II Niuton, ta có:
+ Chọn hệ trục gồm: Ox hướng theo chiều chuyển động của vật: trên mặt phẳng nghiêng, Oy vuông góc với Ox và hướng xuống.
+ Chiếu biểu thức vecto (1) lên trục Ox, Oy ta được:
Theo trục Ox: Px – Fms = ma ⟺ Px – μ.N = ma (2)
Theo trục Oy: Py - N = 0 (3) (theo trục Oy vật không có gia tốc)
Thế (3) vào (2):
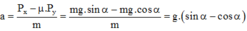
Kết quả cho thấy gia tốc a của vật trượt có ma sát trên mặt phẳng nghiêng phụ thuộc vào g, μ, α.