Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
Áp dụng công thức
![]()
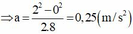
Khi có lực ma sát ta có
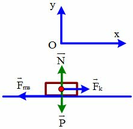
Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động
Áp dụng định luật II Newton ![]()
Chiếu lên trục Ox: ![]()
Chiếu lên trục Oy:
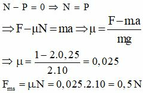
B
Tính a
tính vận tốc áp dụng công thức liên hệ '
my = F*a / m*g

a. Chọn chiều dương là chiều chuyển động.
Theo định luật II Newton P → + N → + F → = m a →
Chiếu lên ox ta có F = m a ⇒ a = F m = 1 2 = 0 , 5 m / s 2
Mà v = v 0 + a t = 0 + 0 , 5.4 = 2 m / s
Áp dụng công thức v 2 − v 0 2 = 2 a s ⇒ a = 2 2 − 0 2 2.8 = 0 , 25 m / s 2
Khi có lực ma sát ta có
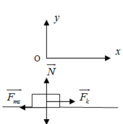
Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động .Áp dụng định luật II Newton. Ta có F → + F → m s + N → + P → = m a →
Chiếu lên trục Ox: F − F m s = m a 1
Chiếu lên trục Oy: N − P = 0 ⇒ N = P
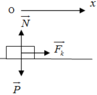
⇒ F − μ N = m a ⇒ μ = F − m . a m g
⇒ μ = 1 − 2.0 , 25 2.10 = 0 , 025
Mà F m s = μ . N = 0 , 025.2.10 = 0 , 5 N

Theo định luật ll Niuton: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\)
Độ lớn lực kéo:
\(F=m.a+F_{ms}=m.a+\mu mg=50\cdot0,5+0,1\cdot50\cdot10=75N\)

a/ \(F_k-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k-m.a}{mg}=...\)
b/ \(F_k.\cos30^0-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k.\cos30^0-m.a}{mg}\)

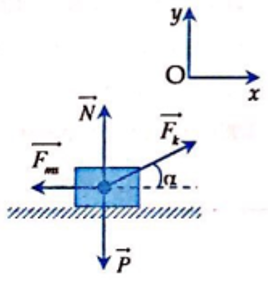
Theo định luật ll Niu tơn:
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{F_k}=m\cdot\overrightarrow{a}\)
\(Oy:N-P-F_k\cdot sin\alpha=0\) \(\Rightarrow N=P-F_k\cdot sin\alpha=m\cdot g-F_ksin\alpha=2\cdot10-F_k\cdot sin30\)
\(\Rightarrow F_{ms}=\mu\cdot N=0,1\cdot\left(20-\dfrac{1}{2}F_k\right)\)
\(Ox:F_k\cdot cos\alpha-F_{ms}=m\cdot a\)
\(\Rightarrow F_k\cdot cos30-F_{ms}=2\cdot a\)
\(\Rightarrow a=???\)
Vì đề bài ko cho \(F\) bằng bao nhiêu nên mình ko thay số đc nhé

a/ \(F_k-F_{ms}=m.a\Rightarrow a=\dfrac{F_k-\mu mg}{m}=\dfrac{2-0,25.0,5.10}{0,5}=1,5\left(m/s^2\right)\)
b/ \(v=v_0+at=1,5.8=12\left(m/s\right)\)
\(F_{ms}=m.a'\Rightarrow a'=-\dfrac{0,25.0,5.10}{0,5}=-2,5\left(m/s^2\right)\)
\(v''^2-v^2=2aS\Rightarrow S=\dfrac{0-12^2}{2.\left(-2,5\right)}=28,8\left(m\right)\)
\(28,8=vt+\dfrac{1}{2}.a't^2=12.t+\dfrac{1}{2}.\left(-2,5\right).t^2\Rightarrow t=...\left(s\right)\)
\(\Rightarrow S'=v\left(t-1\right)+\dfrac{1}{2}.a'\left(t-1\right)^2=...\left(m\right)\)
\(\Rightarrow\Delta S=S-S'=...\left(m\right)\)