Có 2 dãy ghế ngồi đối diện nhau, mỗi dãy có 3 ghế. Xếp ngẫu nhiên 6 học sinh, 3 nam 3 nữ ngồi vô 2 dãy ghế đó s/c mỗi ghế có đúng một học sinh ngồi. Xs để mỗi học sinh nam ngồi đối diện với 1 hs nữ là?
Xép ngẫu nhiên 10 hs gồm 2 hs lớp 12A, 3 hs lớp 12B, 5 hs lớp 12C thành 1 hàng ngang. Xs để 10 hs trên ko có 2 hs nào cùng lớp đứng cạnh nhau là?

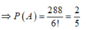





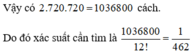


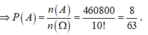

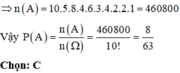
Số phần tử của không gian mẫu là n(Ω) = 6!
Gọi A là biến cố 'nam ngồi đối diện nữ.'
Chọn chỗ cho học sinh nam thứ nhất có 6 cách.
Chọn chỗ cho học sinh nam thứ 2 có 4 cách (không ngồi đối diện học sinh nam thứ nhất)
Chọn chỗ cho học sinh nam thứ 3 có 2 cách (không ngồi đối diện học sinh nam thứ nhất, thứ hai).
Xếp chỗ cho 3 học sinh nữ : 3! cách.
=> n(A) = 6.4.2.3! = 288
Vậy P(A) = 288/6!