Tìm m để pt sau có nghiệm: \(\sqrt{x^2-2mx+1}=m-2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x^2-2mx+m^2-3m+2>0\)
\(\dfrac{x}{\sqrt{x^2-2mx+m^2-3m+2}}=\sqrt{x^2-2mx+m^2-3m+2}\)
- Với \(x< 0\Rightarrow\left\{{}\begin{matrix}VT< 0\\VP>0\end{matrix}\right.\) pt vô nghiệm
- Với \(x\ge0\)
\(\Rightarrow x=x^2-2mx+m^2-3m+2=0\)
\(\Rightarrow x^2-\left(2m+1\right)x+m^2-3m+2=0\) (1)
+ Với \(m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\)
\(m=1\Rightarrow x^2-3x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\) có 2 nghiệm (ktm)
\(m=2\Rightarrow x^2-5x=0\Rightarrow x=\left\{0;5\right\}\) ktm
+ Với \(m^2-3m+2\ne0\)
\(\Rightarrow\) pt đã cho có nghiệm duy nhất khi \(\left(1\right)\) có đúng 1 nghiệm dương
\(\Rightarrow x_1x_2=m^2-3m+2< 0\)
\(\Rightarrow1< m< 2\)

a thay vào mà tính, dễ rồi nên mình ko làm nữa nhé
b, Để phương trình có 2 nghiệm phân biệt thì delta > 0
hay \(4m^2-4\left(m-2\right)\left(m-4\right)=4m^2-4\left(m^2-6m+8\right)=6m-8>0\)
\(\Leftrightarrow-8>-6m\Leftrightarrow m>\dfrac{4}{3}\)
c, Theo Vi et ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{2m}{m-4}\\x_1x_2=\dfrac{c}{a}=\dfrac{m-2}{m-4}\end{matrix}\right.\)
Lại có: \(\left(x_1+x_2\right)^2=\dfrac{4m^2}{\left(m-4\right)^2}\Rightarrow x_1^2+x_2^2=\dfrac{4m^2}{\left(m-4\right)^2}-2x_1x_2\)
\(=\dfrac{4m^2}{\left(m-4\right)^2}-\dfrac{2m-4}{m-4}=\dfrac{4m^2-\left(2m-4\right)\left(m-4\right)}{\left(m-4\right)^2}\)
\(=\dfrac{4m^2-2m^2+12m-16}{\left(m-4\right)^2}=\dfrac{2m^2+12m-16}{\left(m-4\right)^2}\)

3.
Phương trình có 2 nghiệm khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta=m^2-12\left(m+1\right)\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ne-1\\\left[{}\begin{matrix}m\ge6+4\sqrt{3}\\m\le6-4\sqrt{3}\end{matrix}\right.\end{matrix}\right.\) (1)
Khi đó theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{m}{m+1}\\x_1x_2=\dfrac{3}{m+1}\end{matrix}\right.\)
Hai nghiệm cùng lớn hơn -1 \(\Rightarrow-1< x_1\le x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1+1\right)\left(x_2+1\right)>0\\\dfrac{x_1+x_2}{2}>-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2+x_1+x_1+1>0\\x_1+x_2>-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{m+1}-\dfrac{m}{m+1}+1>0\\-\dfrac{m}{m+1}>-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{m+1}>0\\\dfrac{m+2}{m+1}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>-1\\\left[{}\begin{matrix}m>-1\\m< -2\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m>-1\)
Kết hợp (1) \(\Rightarrow\left[{}\begin{matrix}-1< m< 6-4\sqrt{3}\\m\ge6+4\sqrt{3}\end{matrix}\right.\)
Những bài này đều là dạng toán lớp 10, thi lớp 9 chắc chắn sẽ không gặp phải
1. Có 2 cách giải:
C1: đặt \(f\left(x\right)=x^2+2mx-3m^2\)
\(x_1< 1< x_2\Leftrightarrow1.f\left(1\right)< 0\Leftrightarrow1+2m-3m^2< 0\Rightarrow\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\)
C2: \(\Delta'=4m^2\ge0\) nên pt luôn có 2 nghiệm
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=-3m^2\end{matrix}\right.\)
\(x_1< 1< x_2\Leftrightarrow\left(x_1-1\right)\left(x_2-1\right)< 0\)
\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1< 0\)
\(\Leftrightarrow-3m^2+2m+1< 0\Rightarrow\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\)

(m-1)x2-2mx+m-2=0(m\(\ne1\) )
\(\Delta\)'=\(m^2-\left(m-2\right)\left(m-1\right)\)
=\(m^2-m^2+m+2m-2\)
=3m-2
Để pt có nghiệm 2 ngiệm trái dấu thì \(\Delta\) ' =3m-2>0\(\Leftrightarrow m>\dfrac{2}{3}\)
Áp dụng hệ thức Viet, ta có
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2m}{m-1}\\x_1.x_2=\dfrac{m-2}{m-1}\end{matrix}\right.\)
Để PT có 2 nghiệm trái dấu thì x1x2<0\(\Leftrightarrow\dfrac{m-2}{m-1}< 0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m-2< 0\\m-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}m-2>0\\m-1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\)\(\left[{}\begin{matrix}\left\{{}\begin{matrix}m< 2\\m>1\end{matrix}\right.\\\left\{{}\begin{matrix}m>2\\m< 1\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow1< m< 2\)
Vậy 1<m<2 thì pt có 2 nghiệm trái dấu
câu b
.Với m=1\(\Rightarrow-2x-1=0\Leftrightarrow x=\dfrac{-1}{2}\left(l\right)\)
.Với \(m\ne1\)
\(\Rightarrow\Delta\)'=3m-2\(\ge0\Leftrightarrow m\ge\dfrac{2}{3}\)

a) thay m=5 vào pt (1) dc
\(\left(5-4\right)x^2-2.5x+5-2=0\)
<=>\(x^2-10x+3=0\)
<=>\(\left(x-5-\sqrt{22}\right)\left(x-5+\sqrt{22}\right)=0\)
<=>\(\left[{}\begin{matrix}x=5+\sqrt{22}\\x=5-\sqrt{22}\end{matrix}\right.\)
b)Thay x=-1 vào pt (1) dc
\(\left(m-4\right)\left(-1\right)^2-2m\left(-1\right)+m-2=0\)
<=>\(m-4+2m+m-2=0\)
<=>\(4m=6\)
<=>m=\(\dfrac{3}{2}\)
Pt có nghiệm nên
Áp dụng hệ thức Vi-ét ta có
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2m}{m-4}\left(2\right)\\x_1.x_2=\dfrac{m-2}{m-4}\left(3\right)\end{matrix}\right.\)
Thay m=\(\dfrac{3}{2}\)và x=-1 vào pt (2) ta dc
\(-1+x=\dfrac{2.\dfrac{3}{2}}{\dfrac{3}{2}-4}=-\dfrac{6}{5}\)
=>x=\(-\dfrac{1}{5}\)
c)\(\Delta'=\left[-\left(m\right)\right]^2-\left(m-4\right)\left(m-2\right)=m^2-\left(m^2-6m+8\right)=6m-8\)
pt có nghiệm kép <=>\(\Delta'=0\)
<=>\(6m-8=0< =>m=\dfrac{4}{3}\)

\(\text{Δ}=\left(-2m\right)^2-4\left(m-1\right)\left(m+1\right)\)
\(=4m^2-4m^2+4=4\)
Vì Δ>0 nên phương trình luôn có hai nghiệm phân biệt
Theo đề, ta có:
\(\left\{{}\begin{matrix}x_1-2x_2=0\\x_1+x_2=\dfrac{2m}{m-1}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_2=\dfrac{2m}{m-1}\\x_1=2x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{2m}{3m-3}\\x_1=\dfrac{4m}{3m-3}\end{matrix}\right.\)
Theo đề, ta có: \(x_1\cdot x_2=\dfrac{m+1}{m-1}\)
\(\Leftrightarrow\dfrac{8m^2}{9\left(m-1\right)^2}=\dfrac{m+1}{m-1}\)
\(\Leftrightarrow8m^2=9\left(m+1\right)\left(m-1\right)\)
\(\Leftrightarrow9m^2-9-8m^2=0\)
hay \(m\in\left\{3;-3\right\}\)
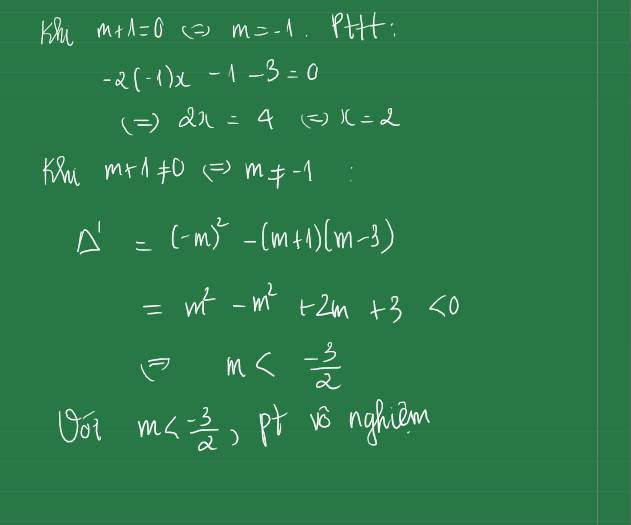
\(pt\Leftrightarrow\left\{{}\begin{matrix}x^2-2mx+1=m^2-4m+4\\m-2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-2mx-m^2+4m-4=0\left(1\right)\\m\ge2\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(\left(1\right)\) có nghiệm và \(m\ge2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=2\left(m-1\right)^2+2\ge0\\m\ge2\end{matrix}\right.\)
\(\Leftrightarrow m\ge2\)