Cho hàm số y= -1/3x và hàm số y= x-4
a, Vẽ đồ thị hàm số y= -1/3x
b, Chứng tỏ M(3;-1) là giao của hai đồ thị hàm số trên.
c, Tính độ dài OM ( O là gốc tọa độ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 12 2021
\(a,\Leftrightarrow2\left(4a-1\right)=6\Leftrightarrow4a-1=3\Leftrightarrow a=1\\ b,\text{Gọi }y=ax+b\text{ là đt đi qua }M,N\\ \Leftrightarrow\left\{{}\begin{matrix}a+b=-3\\-\dfrac{1}{3}a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=0\end{matrix}\right.\Leftrightarrow y=-3x\\ \text{Thay }x=-\dfrac{1}{3};y=-1\Leftrightarrow-1=-3\left(-\dfrac{1}{3}\right)=1\left(\text{vô lí}\right)\\ \Leftrightarrow P\notin y=-3x\\ \text{Thay }x=-\dfrac{1}{2};y=1,5=\dfrac{3}{2}\Leftrightarrow\dfrac{3}{2}=\left(-3\right)\left(-\dfrac{1}{2}\right)=\dfrac{3}{2}\left(\text{nhận}\right)\\ \Leftrightarrow Q\in y=-3x\)
Vậy M,N,Q thẳng hàng
3 tháng 1 2024
a: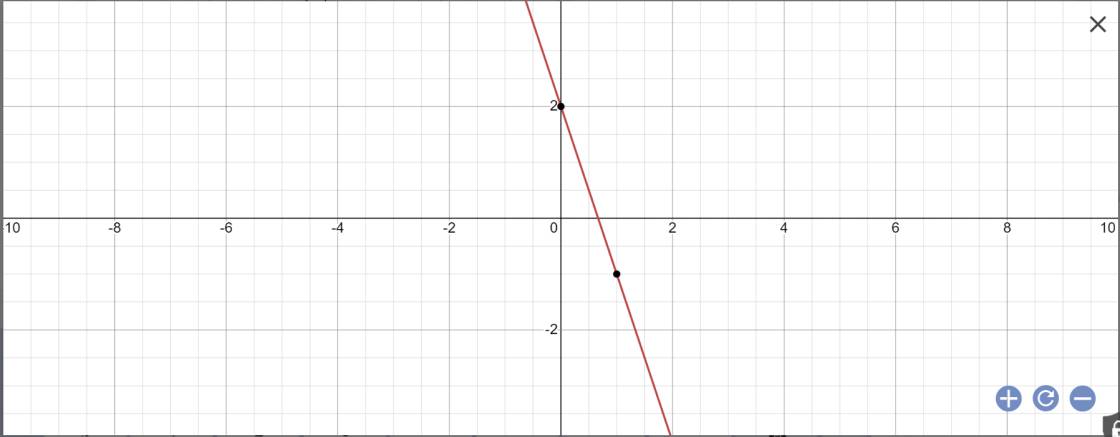 
b: Để đồ thị hàm số y=(m+1)x-3 song song với đồ thị hàm số y=-3x+2 thì \(\left\{{}\begin{matrix}m+1=-3\\2\ne-3\left(đúng\right)\end{matrix}\right.\)
=>m+1=-3
=>m=-4
17 tháng 8 2023
2:
a: Thay x=0 và y=-3 vào (d), ta được:
3*0+b=-3
=>b=-3
b: Thay x=-4 và y=0 vào (d), ta được:
3*(-4)+b=0
=>b=12
c: Thay x=-1 và y=2 vào (d), ta được:
3*(-1)+b=2
=>b-3=2
=>b=5
C
21 tháng 3 2017
y=-x/3 y=x-4 M O x y
Giao điểm 2 đồ thị
y=-x/3 và y=x-4
=> -x/3 = x - 4
=> -x = 3x - 12
=> x = 3
Thay x = 3 vào 1 trong 2 hàm số => y = -1
=> M(3,-1) Là giao điểm 2 đồ thị.
OM = \(\sqrt{3^2+\left(-1\right)^2}\) = \(\sqrt{10}\)
TM
5 tháng 9 2023
1. Đồ thị của hàm số đi qua điểm \(M\left(2;3\right)\) nên giá trị hoành độ và tung độ của \(M\) là nghiệm của phương trình đường thẳng trên, tức:
\(3=m\cdot2+m-6\Leftrightarrow m=3\left(TM\right)\)
2. Đồ thị hàm số song song với đường thẳng \(\left(d\right):y=3x+2\), khi: \(\left\{{}\begin{matrix}m=3\\m-6\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne8\end{matrix}\right.\Rightarrow m=3\left(TM\right)\)
3. Gọi \(P\left(x_0;y_0\right)\) là điểm cố định mà đồ thị hàm số đi qua với mọi giá trị \(m\).
Khi đó: \(mx_0+m-6=y_0\Leftrightarrow\left(x_0+1\right)m-\left(y_0+6\right)=0\left(I\right)\)
Suy ra, phương trình \(\left(I\right)\) có vô số nghiệm, điều này xảy ra khi: \(\left\{{}\begin{matrix}x_0+1=0\\y_0+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-6\end{matrix}\right.\).
Vậy: Điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị \(m\) là \(P\left(-1;-6\right)\).