Một trạm điều động xe có 15 xe ô tô trong đó có 10 xe tốt và 5 xe không tốt. Trạm xe điều động ngẫu nhiên 4 xe ô tô đi chở khách, tính xác suất để trong 4 xe ô tô có ít nhất 1 xe tốt?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


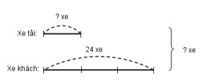
Số xe tải là:
24 : 3 = 8 (xe)
Tổng số xe có trong đội xe là:
24 + 8 = 32 (xe)
Đáp số: 32 xe.

Nếu dùng 4 ô tô thì mới chở được 40 x 4 = 160 (người)
Vậy còn 195 - 160 = 35 (người)
Khi đó cần thêm 1 xe ô tô nữa là chở hết
Số ô tô cần dùng để chở hết 195 người đi dự hội nghị là: 4 + 1 = 5 (ô tô)

Khối lượng hàng mà 3 xe đầu chở là:
\(3\cdot13580=40740\left(kg\right)\)
Khối lượng hàng mà 2 xe sau chở là:
\(15275\cdot2=30550\left(kg\right)\)
Tổng khối lượng hàng 5 xe chở là:
\(40740+30550=71290\left(kg\right)\)
Trung bình mỗi xe chở được là:
\(\dfrac{71290}{5}=14258\left(kg\right)\)

Nếu dùng 4 ô tô thì chở được số người là: 40 x 4 = 160 (người)
Số người còn lại là: 195 – 160 = 35 (người) thì cần 1 xe ô tô nữa là chở hết.
Vậy số ô tô cần dùng là: 4 + 1 = 5 (ô tô)
Đáp số: 5 ô tô
Ít nhất 1 xe tốt, vậy nhiều nhất là 4 xe tốt :)
TH1: 1 xe tốt \(C^1_{10}.C^3_5\) (cách)
TH2: 2 xe tốt \(C^2_{10}.C^2_5\) (cách)
TH3: 3 xe tốt \(C^3_{10}.C^1_5\) (cách)
TH4: 4 xe tốt \(C^4_{10}.C^0_5\) (cách)
\(\Rightarrow n\left(A\right)=C^1_{10}.C^3_5+C^2_{10}.C^2_5+C^3_{10}.C^1_5+C^4_{10}.C^0_5=...\)
Không gian mẫu: \(n\left(\Omega\right)=C^4_{15}\)
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)