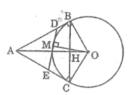
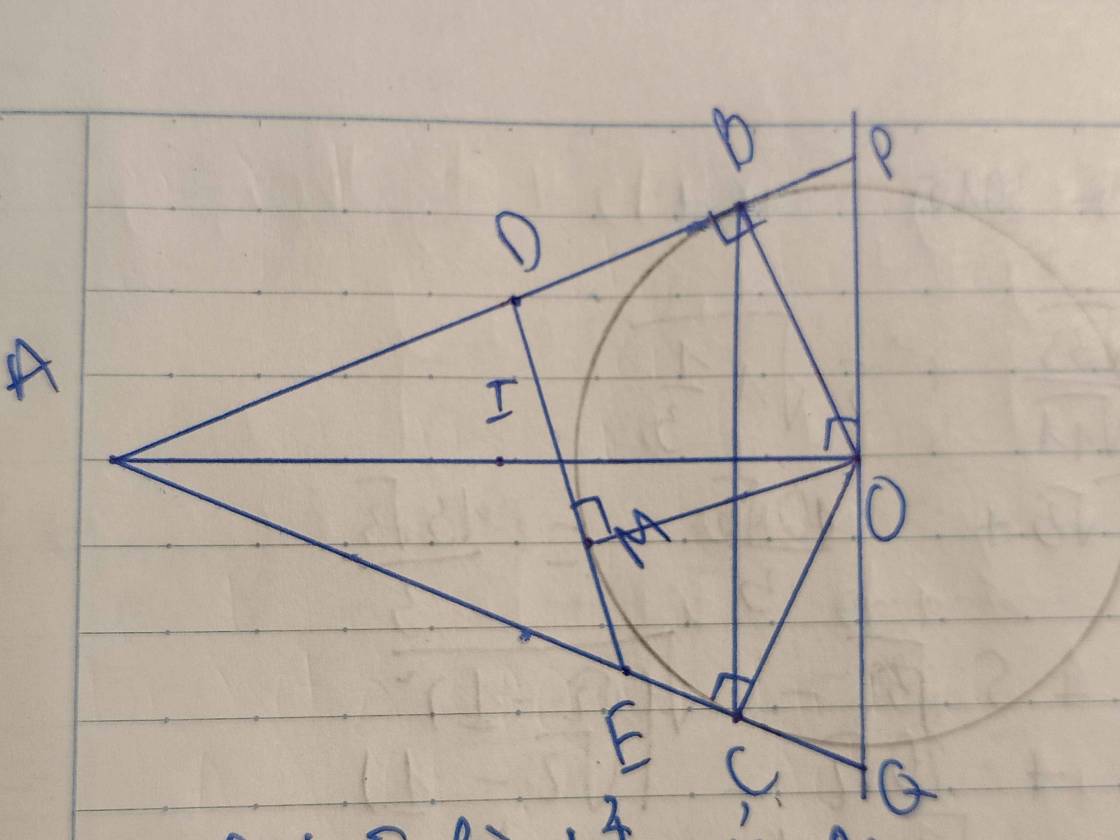
Cho A nằm ngoài đường tròn (O) kẻ tiếp tuyến AB,AC với đường tròn O có B,C là tiếp điểm
a)Cm AO vuông góc BC
b)Trên cung nhỏ BC lấy điểm M bất kì(M khác B,C,OA).Điểm M cắt AB và AC tại D và E.Cm chu vi tam giác ADE=2AB
c)Đường thẳng vuông góc AO tại O cắt AB,AC tại P và Q.CM 4PD.QE=PQ.PQ