cho tam giác abc vuông tại a cs gcs b =35 độ
a , tính góc c
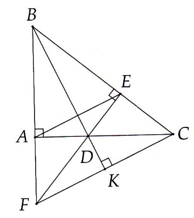
b trên cạch bc lấy điểm d sao cho bd = ba tai phân giác của góc b cắt ac ở điểm e. cmr tam giác bea = tam giác bed
c, qua c, vẽ đg thẳng vuông tại be tại h.ch cắt đg thẳng ab tại f .cmr chia bf
=bc


a . Xét ΔABC ⊥ tại A , ta có :
\(\widehat{ABC} \) + \(\widehat{ACB}\) = 90o ( 2 góc nhọn phụ nhau )
35o + \(\widehat{ACB}\) = 90o
⇒ \(\widehat{ACB}\) = 55o
b . Xét ΔBEA và ΔBED, ta có :
\(\left\{{}\begin{matrix}BA=BD\left(gt\right)\\\widehat{ABE}=\widehat{DBE}\\BE-BE\end{matrix}\right.\)
⇒ ΔBEA = ΔBED ( cạnh chung )
thêm vào chỗ góc ABE = góc DBE là ( BE là tia pg của góc ABC ) và BE=BE ( cạnh chung ) hộ mình nhá :3