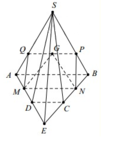
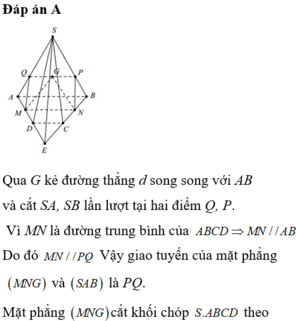
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm của tam giác SAB; I và M lần lượt là trung điểm của AB và SD.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
b) Gọi N là giao điểm DI và AC. Chứng minh rằng NG song song với (SCD)
c)Tìm giao điểm E của SO và (CGM). Tính tỉ số \(\frac{SE}{SO}\)