Thực hiện phép tính : ( p/s : B1 : tìm mẫu thức chung MTC , B2 : Lấy MTC nhân MT riêng , B3 : đặt chung 1 mẫu thức còn tử thì phân tích , B4 : rút gọn với mẫu )
Giải dùm \(\frac{x+1}{x-2}+\frac{8-7x}{x^2-2x}+\frac{2}{x}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{x^2+x}=\dfrac{x-1}{x\left(x-1\right)\left(x+1\right)};\dfrac{x^2-4}{x^2-1}=\dfrac{x\left(x^2-4\right)}{x\left(x-1\right)\left(x+1\right)}\\ \dfrac{1}{y-1}-\dfrac{1}{y}=\dfrac{y-y+1}{y\left(y-1\right)}=\dfrac{1}{y\left(y-1\right)}\)

Cả hai bạn đều làm đúng.
- Bạn Tuấn trực tiếp đi tìm mẫu thức chung theo quy tắc:
x3 – 6x2 = x2(x – 6)
x2 – 36 = x2 – 62 = (x – 6)(x + 6)
MTC = x2(x – 6)(x + 6).
- Bạn Lan rút gọn phân thức trước khi đi tìm mẫu thức chung:
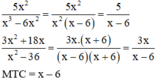
MTC = x – 6
\(\Leftrightarrow\)\(\frac{x+1}{x-2}+\frac{8-7x}{x^2-2x}+\frac{2}{x}\left(ĐKXĐ.x\ne2.x\ne0\right)\)
\(\Leftrightarrow\)\(\frac{x\left(x+1\right)}{x\left(x-2\right)}+\frac{8-7x}{x\left(x-2\right)}+\frac{2\left(x-2\right)}{x\left(x-2\right)}\)
\(\Leftrightarrow\frac{x^2+x+8-7x+2x-4}{x\left(x-2\right)}\)
\(\Leftrightarrow\frac{x^2-4x+4}{x\left(x-2\right)}\)
\(\Leftrightarrow\frac{\left(x-2\right)^2}{x\left(x-2\right)}\Leftrightarrow\frac{x-2}{x}\)