Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\widehat{B}=180^o-60^o-45^o=75^o\)
Theo định lý sin ta có:
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\)
\(\Rightarrow AC=\dfrac{AB\cdot sinB}{sinC}=\dfrac{5\cdot sin75^o}{sin45^o}=\dfrac{5+5\sqrt{3}}{2}\)
Mà: \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot5\cdot\dfrac{5+5\sqrt{3}}{2}\cdot sin60^o=\dfrac{75+25\sqrt{3}}{8}\left(dvdt\right)\)

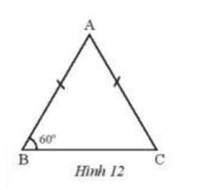
Ta có: tam giác ABC cân tại A
Nên \(\widehat B = \widehat C = {60^o}\)( 2 góc đáy của tam giác cân )
Theo định lí về tổng 3 góc trong tam giác ta có : \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat A = {180^o} - {60^o} - {60^o} = {60^o}\)
Vì \(\widehat A = \widehat B = \widehat C = {60^o}\)\( \Rightarrow \) tam giác ABC là tam giác đều

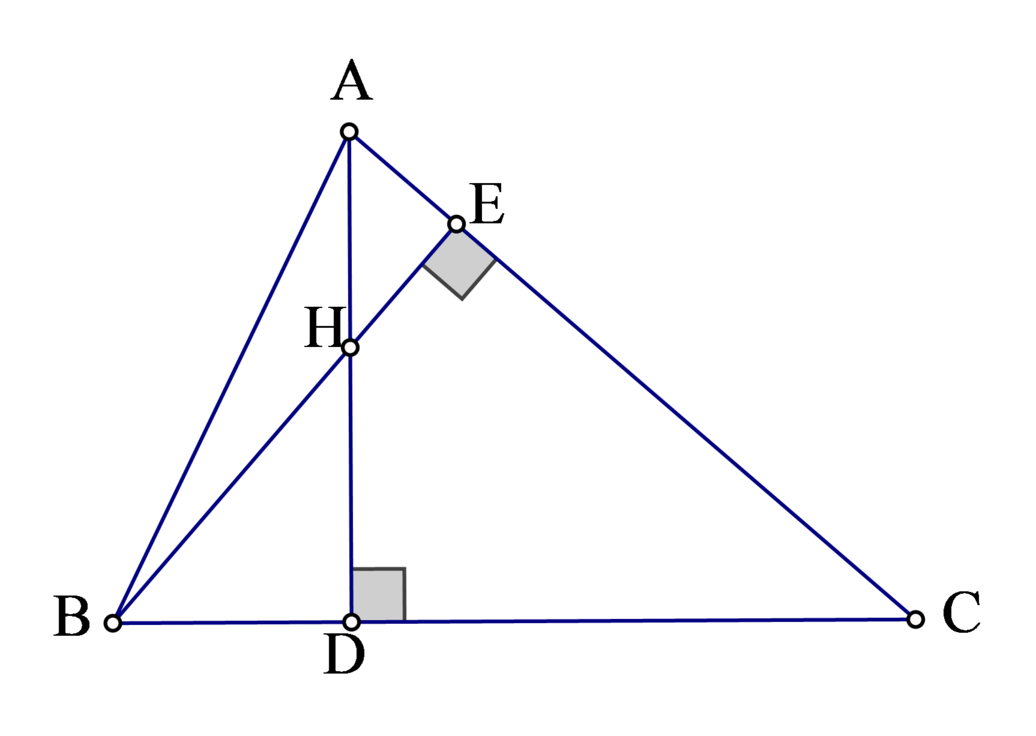
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
mà EH là đường cao
nên H là trung điểm của BC
=>HB=HC
d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEI=góc HEC
=>ΔEAI=ΔEHC
=>EI=EC>EH

\(a,AB=\cos B\cdot BC=6\left(cm\right)\\ AC=\sqrt{BC^2-AB^2}=6\sqrt{3}\left(cm\right)\\ b,\text{Áp dụng HTL: }AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{3}\left(cm\right)\)
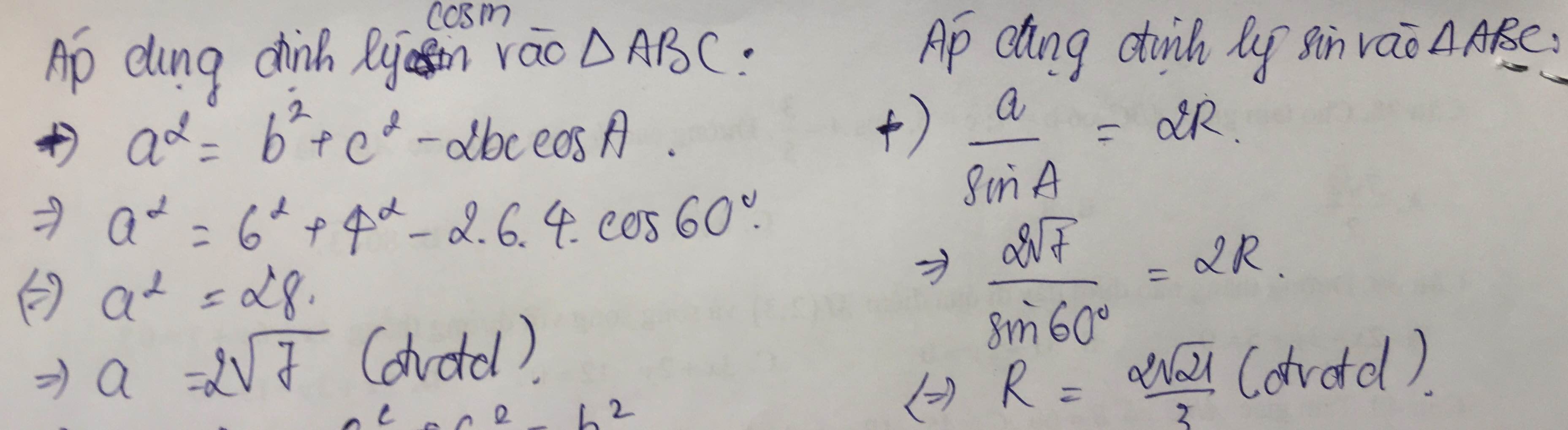
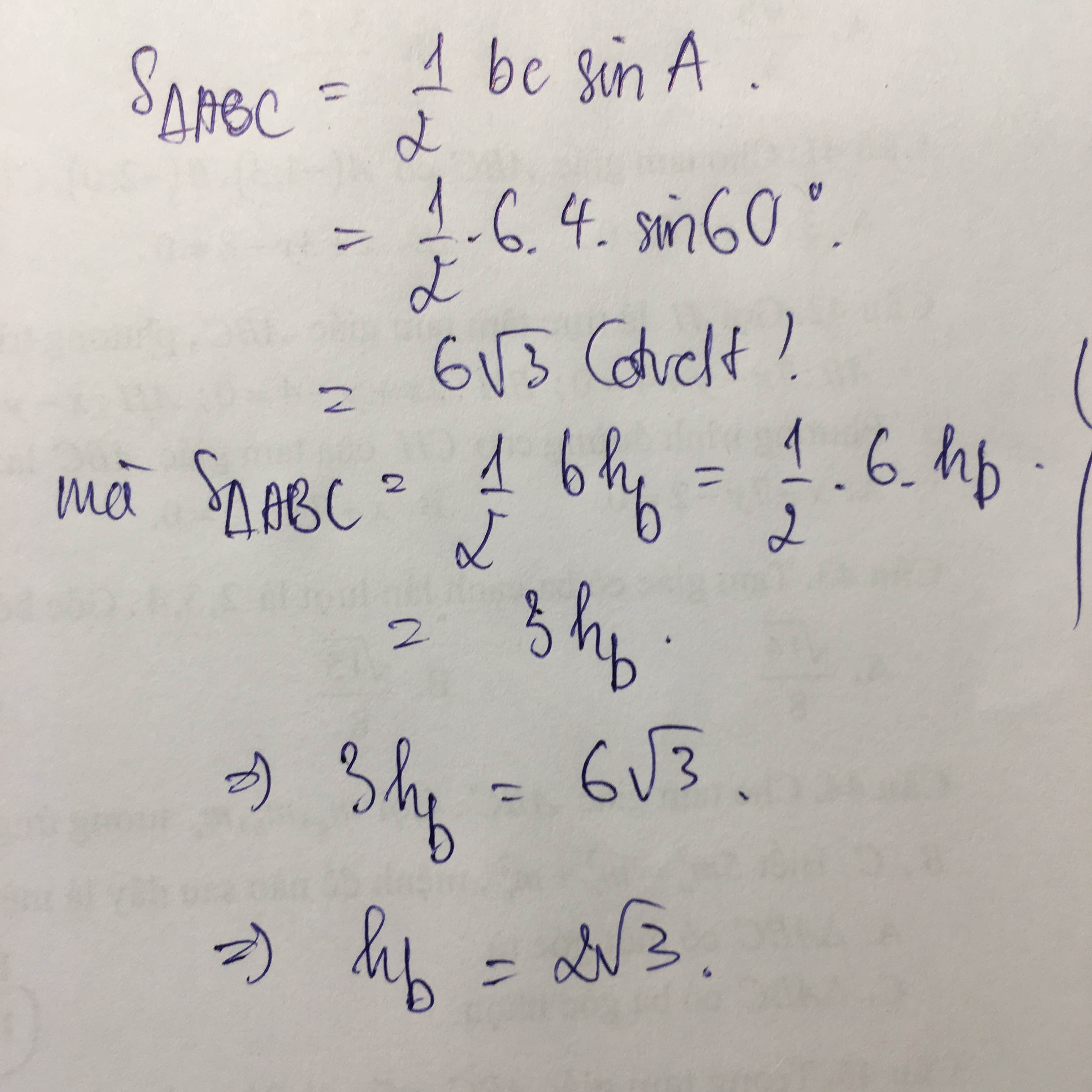
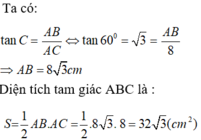
a) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}=180^0-\widehat{A}-\widehat{C}\)
\(\Leftrightarrow\widehat{B}=180^0-60^0-40^0\)
hay \(\widehat{B}=80^0\)
Vậy: \(\widehat{B}=80^0\)
b) Xét ΔAEB và ΔCED có
AE=CE(E là trung điểm của AC)
\(\widehat{AEB}=\widehat{CED}\)(hai góc đối đỉnh)
EB=ED(gt)
Do đó: ΔAEB=ΔCED(c-g-c)
c) Xét ΔAED và ΔCEB có
AE=CE(E là trung điểm của AC)
\(\widehat{AED}=\widehat{CEB}\)(hai góc đối đỉnh)
ED=EB(gt)
Do đó: ΔAED=ΔCEB(c-g-c)
\(\Rightarrow\widehat{EAD}=\widehat{ECB}\)(hai góc tương ứng)
mà \(\widehat{EAD}\) và \(\widehat{ECB}\) là hai góc ở vị trí so le trong
nên AD//BC(Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: AD//BC(cmt)
\(EH\perp BC\)(gt)
Do đó: \(EH\perp AD\)(Định lí 2 từ vuông góc tới song song)