Cho phân số a/b và phân số a/c có b+c=a (a,b,c thuộc Z, b khác 0, c khác 0).
Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng. Thử lại với a=8, b-3.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 4 2017
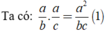
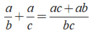
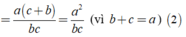
Từ (1), (2) ta có:
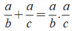với b + c = a (a, b, c ∈ Z, b ≠ 0, c ≠ 0)
Nếu a = 8, b = -3 thì c = a - b = 8 - (-3) = 11
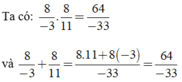
ta có: \(\frac{a}{b}.\frac{a}{c}=\frac{a}{b}+\frac{a}{c}\Leftrightarrow\frac{a^2}{bc}=\frac{ac}{bc}+\frac{ab}{bc}=\frac{ab+ac}{bc}\Leftrightarrow ab+ac=a^2\Leftrightarrow a\left(b+c\right)=a^2\Leftrightarrow a^2=a^2\)
=>đpcm
*thử lại với a=8;b=-3:tự làm