Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Answer:
Phần c) thì nhờ các cao nhân khác thoii.
a) Ta xét tam giác ABD và tam giác EBD:
AB = EB (gt)
BD cạnh chung
\(\widehat{B_1}=\widehat{B_2}\)
Vậy tam giác ABD = tam giác EBD (c.g.c)
\(\Rightarrow DE=DA\)
b) Theo phần a), tam giác ABD = tam giác EBD
\(\Rightarrow\widehat{BAD}=\widehat{BED}=90^o\)

Xét ΔABDΔABD và ΔEBDΔEBD, ta có:
AB=BE ( gt)
ABDˆ=EBDˆABD^=EBD^ ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD⇒ΔABD=ΔEBD (c-g-c)

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>\(\widehat{BED}=\widehat{BAD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
b: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔDAF=ΔDEC
=>DF=DC

a/ Xét \(\Delta ABD\)và \(\Delta EBD\)
BA=BE (gt); BD chung
\(\widehat{ABD}=\widehat{EBD}\)(gt)
\(\Rightarrow\Delta ABD=\Delta EBD\left(c.g.c\right)\)
b/
\(\Delta ABD=\Delta EBD\left(cmt\right)\Rightarrow\widehat{BAD}=\widehat{BED}=90^o\Rightarrow DE\perp BC\)
c/
Ta có
BE=BA (gt); AF=CE (gt)
=> BE+CE=BA+AF => BC=BF => tg BCF cân tại B
Mà BD là phân giác \(\widehat{ABC}\)
\(\Rightarrow BD\perp CF\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
Mà \(CA\perp BF\)
=> D là trực tâm của \(\Delta BCF\Rightarrow FD\perp BC\) mà \(DE\perp BC\) => FD trùng DE (từ 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng vuông góc với đường thẳng đã cho) => E, D, F thẳng hàng
hình vào tcn cho mình thay G là điểm D vì mình nhầm trọng tâm của tam giác
a) Xét tam giác ABD và tam giác EBD có:
AB=BE (gt)
^ABD=^EBD (^ABD là tia phân giác)
BD chung
=> tam giác ABD = tam giác EBD ( c.g.c )
b) Vì ABC là tam giác vuông tại A
=> tam giác ABD là tam giác vuông tại A
Mà: tam giác ABD = tam giác EBD ( c.g.c )
=> ^BED=^BAD= 90o
=> DE_|_BC (đpcm)
c) Nối F và C lại với nhau
Vì: FA=FB ( gt)
Mà CA_|_FB ( tam giác ABC _|_ tại A)
=> CA là đg trung trực của tam giác ABC
=> CA là đg trung tuyến của tam giác ABC
Mà tia phân giác ABC cắt AC tại D
=> D là trọng tâm của tam giác ABC
=> D,E,F thằng hàng (đpcm)

a) Xét tam giác ABD và tam giác EBD:
+ AB = EB (gt).
+ BD chung.
+ \(\widehat{ABD}=\widehat{EBD}\) (BD là phân giác).
\(\Rightarrow\) Tam giác ABD = Tam giác EBD (c - g - c).
b) Tam giác ABD = Tam giác EBD (cmt).
\(\Rightarrow\) \(\widehat{BAD}=\widehat{BED}\) (2 góc tương ứng).
Mà \(\widehat{BAD}=90^o\) (Tam giác ABC vuông tại A).
\(\Rightarrow\) \(\widehat{BED}=90^o\)
c) Xét tam giác ABE: BA = BE (gt).
\(\Rightarrow\) Tam giác ABE cân tại B.
Mà BD là phân giác (gt).
\(\Rightarrow\) BD là đường cao (Tính chất tam giác cân).
\(\Rightarrow\) \(BD\perp AE.\)

a)Xét tam giác ABD và tam giác EBD có:
AB=BE (gt)
\(\widehat{ABD}\)=\(\widehat{CBD}\)
BD là cạnh chung
Vậy \(\Delta ABD\)= \(\Delta EBD\)(c-g-c)
b) Vì \(\Delta ABD\)= \(\Delta EBD\)(cmt)
Nên \(\widehat{BAD}=\widehat{BED}\)= 90 độ
a , Xét tam giác ABD và tam giác EBD ta có :
cạnh BD chung
góc ABD= góc DBE [ BD là tia p/g của góc ABE ]
BA=BE [ gt ]
=> tam giác ABD = tam giác EBD [ c.g.c ]
b, Vì tam giác ABD= tam giác EBD [ cmt ]
=> góc A = góc EBD [ 2 góc tương ứng ]
Mà góc A = 90 độ
=> góc EBD = 90 độ
chúc bạn học tốt kết bạn với mình nha
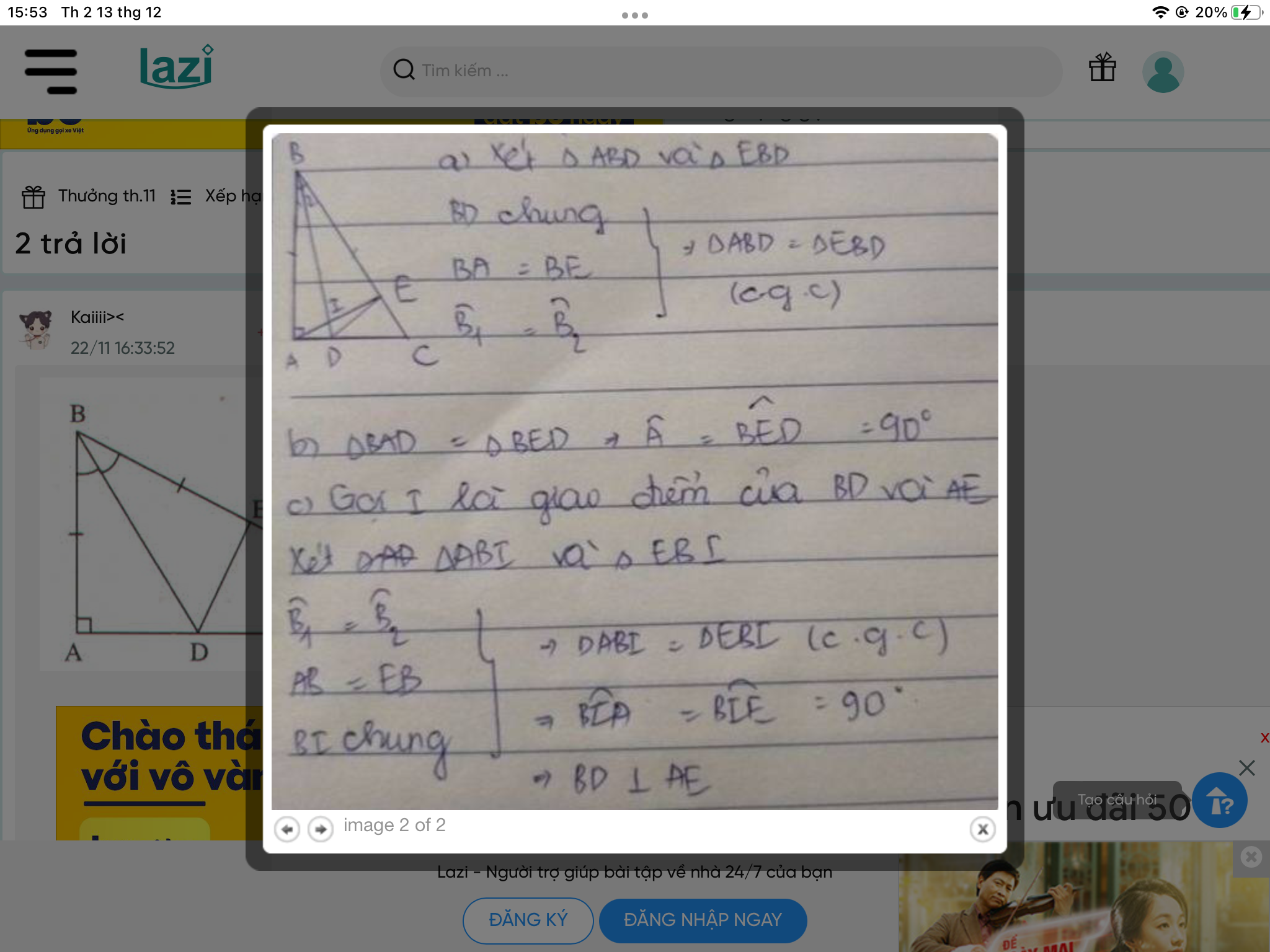
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)