Cho tam giác ABC vuông tại A .Trung tuyến AM. D; E lần lượt là trung điểm của AB; AC. N đối xứng với M qua D. Q đối xứng với N qua A.
a) Tứ giác ADME là hình gì ? Tại sao?
b) Tứ giác ANBM là hình gì ? Tại sao?
c)Tứ giác ANMC là hình gì ? Tại sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M D
a/ Xét tứ giác ABCD có:
M là trung điểm BC
M là trung điểm AD
=> tứ giác ABCD là hình bình hành (Dù nhìn hình không giống vì nó có thể là hcn nhưng dựa vào lý thuyết hoàn toàn chuẩn!)
=> BD//AC
Mà: AB vuông góc AC (gt)
=> AB vuông góc BD
=> tam giác ABD vuông tại B
b/ Xét tam giác ABD và tam giác ABC có:
góc ABD = góc BAC = 90 độ (cmt)
góc ADB = góc ACB (BD//AC, đồng vị)
AB: chung
=> tam giác ABD = tam giác BAC (g.c.g)
Xét tam giác ABC vuông tại A có AM là đường trung tuyến => AM = BM = CM = 1/2 BC (đpcm)
=> AM < BC (thêm cái này đi cho chắc ăn!)

a) Xét ΔMAB và ΔMDC có
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔMAB=ΔMDC(c-g-c)
b) Ta có: ΔMAB=ΔMDC(cmt)
nên \(\widehat{MAB}=\widehat{MDC}\)(hai góc tương ứng)
mà \(\widehat{MAB}\) và \(\widehat{MDC}\) là hai góc ở vị trí so le trong
nên AB//CD(Dấu hiệu nhận biết hai đường thẳng song song)
mà AB⊥AC(gt)
nên DC⊥AC
c) Xét ΔABC vuông tại A và ΔCDA vuông tại C có
CA chung
BA=DC(ΔMAB=ΔMDC)
Do đó: ΔABC=ΔCDA(Hai cạnh góc vuông)
Suy ra: BC=DA(Hai cạnh tương ứng)
mà \(MA=\dfrac{1}{2}DA\)(M là trung điểm của DA)
nên \(MA=\dfrac{1}{2}BC\)
a)
Xét tam giác MAB và tam giác MDC có :
MA = MD( theo giả thiết)
BM = MC ( vì AM là trung tuyến của tam giác ABC)
góc AMB = góc CMD(vì đối đỉnh)
Do đó tam giác MAB = tam giác MCD( c.c.c)
b)
Theo câu a), suy ra góc BAM = góc MDC
Suy ra : AB // CD
mà AB ⊥ AC nên CD ⊥ AC
c)
Vì AM là tia trung tuyến thuộc cạnh huyền BC nên AM = \(\dfrac{1}{2}\)BC
Suy ra : AM = BM = MC
Suy ra: tam giác AMC cân tại M
Do đó góc MAC = góc MCA
Xét tam giác ABC vuông tại A và tam giác CDA vuông tại C, ta có:
Cạnh AC chung
Góc MAC = Góc MCA
Do đó tam giác ABC = tam giác CDA( cạnh huyện- gọc nhọn kề)

Lam truoc cau a nhe,toi roi
a.Vi tu giac AFME co 3 goc vuong va 2 duong cheo vuong goc voi nhau nen AFDE la hinh vuong.
Goi giao diem giua 2 duong cheo AM va EF do la Q
Suy ra:AQ=FQ nen tam giac AQF la tam giac vuong can hay \(\widehat{AQF}=45^0\left(1\right)\)
Tu giac QFKM co 3 goc vuong va MQ=FQ nen QFKM la hinh vuong.
Suy ra:FK=MK
Ta co:\(FK^2=MK.KC\Rightarrow FK=KC\)
Nen tam giac FKC la tam giac vuong can hay \(\widehat{C}=45^0\left(2\right)\)
Tu (1) va (2) suy ra:AM=MC
Hay AM la duong trung tuyen cua tam giac ABC.

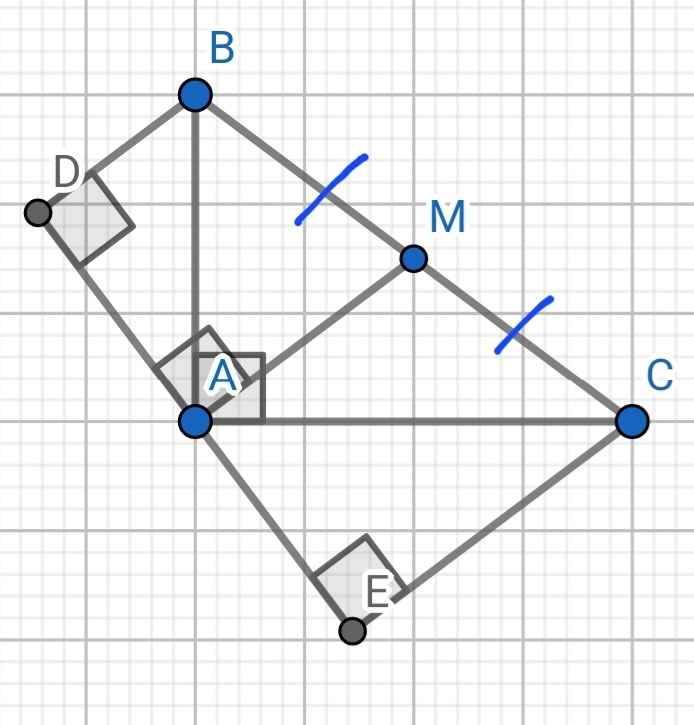
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC
Giải:
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
= 10 : 2 = 5 (cm)
∆AMC có AM = CM = 5 (cm)
⇒ ∆AMC cân tại M
⇒ ∠MAC = ∠MCA (hai góc ở đáy)
Do MA ⊥ DE (gt)
CE ⊥ DE (gt)
⇒ MA // DE
⇒ ∠MAC = ∠ACE (so le trong)
Mà ∠MAC = ∠MCA (cmt)
⇒ ∠MAC = ∠ACE
⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)
Xét hai tam giác vuông:
∆ABC và ∆EAC có:
∠BCA = ∠ACE (cmt)
⇒ ∆ABC ∽ ∆EAC (g-g)
b) Do ∆ABC ∽ ∆EAC (cmt)
⇒ AC/CE = BC/AC
⇒ CE = AC²/BC
= 8²/10
= 6,4 (cm)