Tìm ba cạnh của một tam giác vuông biết độ dài ba cạnh là số nguyên trong đó có một cạnh bằng 7.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi cạnh hình tam giác là a
canh hinh vuông là b
theo đề ta có
a+b=70
ax3=bx4
=>a/b=4/3
số phần là 4+3=7(phần)
cạnh hình tam giác có độ dài là
70:7x4=40
cạnh hình vuông là
70-40=30
ĐS 30cm
40cm

Đáp án A
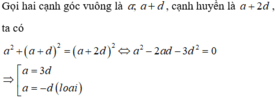
Do đó 3 cạnh của tam giác vuông cần tìm có dạng 3d ;4d ;5d, tức là một cạnh bất kì phải chia hết cho 3, hoặc chia hết cho 4, hoặc chia hết cho 5.
Trong các đáp án, chỉ có số 81 thỏa mãn chia hết cho 3.

gọi :ba cạnh của hình tam giác là a ,b,c
ta có :\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{40,5}{15}=2,7\)
áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{a}{3}=2,7\Rightarrow a=2,7.3=8,1\)
\(\frac{b}{5}=2,7\Rightarrow b=2,7.5=13,5\)
\(\frac{c}{7}=2,7\Rightarrow c=2,7.7=18,9\)
đáp số : 3 cạnh hình vuông có chiều dài là :18,9;13,5;8,1
Gọi độ dài 3 cạnh của 1 tam giác lần lượt là a, b, c (cm)
Theo đề bài ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)
\(a+b+c=40,5\)
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{40,5}{15}=2,7\)
\(\cdot\frac{a}{3}=2,7\Rightarrow a=2,7.3=8,1\)
\(\cdot\frac{b}{5}=2,7\Rightarrow b=2,7.5=13,5\)
\(\cdot\frac{c}{7}=2,7\Rightarrow c=2,7.7=18,9\)
Vậy độ dài 3 cạnh của 1 tam giác lần lượt là 8,1cm; 13,5cm; 18,9cm

Tổng ba cạnh tam giác lúc đầu là : 327,46 cm
Khi tăng cạnh thứ nhất thêm 2,46cm và giảm cạnh thứ hai đi 5,32cm thì tổng ba cạnh của tam giác lúc sau là:
327, 46 + 2,46 - 5,32 = 324,6 (cm)
Mỗi cạnh của tam giác lúc sau bằng nhau và bằng :
324,6 : 3 = 108,2 (cm)
Vì cạnh thứ nhất tăng thêm và cạnh thứ hai giảm đi thì ba cạnh bằng nhau nên cạnh thứ nhất là cạnh bé nhất và có độ dài là:
108,2 - 2,46 = 105,74 (cm)
Cạnh hình vuông cạnh cạnh bé nhất của tam giác và bằng 105,74 cm
Diện tích hình vuông là:
105,74 x 105,74 = 11180,9476 (cm2)
Đs....

TH1: 2 cạnh nguyên tố đó là 2 cạnh góc vuông lần lượt: a;a+50a;a+50
Khi đó, cạnh huyền: a2+(a+50)2−−−−−−−−−−−√=2a2+100a+2500−−−−−−−−−−−−−−−√a2+(a+50)2=2a2+100a+2500
Với a=5 (loại).
Với a khác 5, có: a2≡1or4(mod5)→2a2+100a+2500≡2or3(mod5)a2≡1or4(mod5)→2a2+100a+2500≡2or3(mod5) kg là SCP.
Vậy TH này loại.
TH2: 1 cạnh huyền, 1 cạnh góc vuông: a;a+50a;a+50
Cạnh góc vuông còn lại: (a+50)2−a2−−−−−−−−−−−√=100a+2500−−−−−−−−−−√=10.a+25−−−−−√(a+50)2−a2=100a+2500=10.a+25
Đặt: a+25−−−−−√=t→a+25=t2⇔a=(t−5)(t+5)→t−5=1⇔t=6⇔a=11a+25=t→a+25=t2⇔a=(t−5)(t+5)→t−5=1⇔t=6⇔a=11 (đúng)
Vậy số đo 3 cạnh nhỏ nhất là: 11;60;6111;60;61 (11,61 nguyên tố)
Vậy đáp số giá trị nhỏ nhất của cạnh thứ 3: 60

