x4-mx2+m-1 =0 .Biết m= m0 là giá trị để phương trình có 4 nghiệm phân biệt trong đó hai nghiệm dương thỏa mãn |x1-x2|=1 . Tìm m0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\Delta'=\left(m-2\right)^2+m-2\)
\(=m^2-4m+4+m-2\)
\(=m^2-3m+2\)
Để pt có 2 nghiệm phân biệt thì \(\Delta'>0\Leftrightarrow\orbr{\begin{cases}m< 1\\m>2\end{cases}}\)
Teo Vi-et \(\hept{\begin{cases}x_1+x_2=2\left(m-2\right)\\x_1x_2=-m+2\end{cases}}\)
Ta có \(x_1+2x_2=2\)
\(\Leftrightarrow\left(x_1+x_2\right)+x_2=2\)
\(\Leftrightarrow2\left(m-2\right)+x_2=2\)
\(\Leftrightarrow2m-4+x_2=2\)
\(\Leftrightarrow x_2=6-2m\)
Ta có \(x_1+x_2=2\left(m-2\right)\)
\(\Leftrightarrow x_1+6-2m=2m-4\)
\(\Leftrightarrow x_1=4m-10\)
Thay vào tích x1 . x2 được
\(x_1x_2=-m+2\)
\(\Leftrightarrow\left(4m-10\right)\left(6-2m\right)=-m+2\)
\(\Leftrightarrow24m-8m^2-60+20m=-m+2\)
\(\Leftrightarrow8m^2-45m+62=0\)
Có \(\Delta=41\)
\(\Rightarrow\orbr{\begin{cases}m=\frac{45-\sqrt{41}}{16}\left(tm\right)\\m=\frac{45+\sqrt{41}}{16}\left(tm\right)\end{cases}}\)
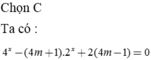

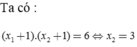
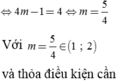
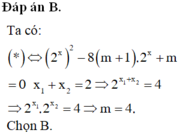
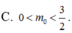



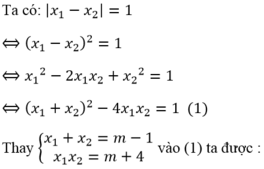
\(x^4-1-mx^2+m=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2+1\right)-m\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=1\\x^2=m-1\end{matrix}\right.\)
Pt có 4 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ne2\end{matrix}\right.\)
Khi đó ta có:
\(\left|x_1-x_2\right|=\left|1-\sqrt{m-1}\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}1-\sqrt{m-1}=1\\1-\sqrt{m-1}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\left(loại\right)\\m=5\end{matrix}\right.\)
Vậy \(m_0=5\)