Giúp mik bài hình với
ll nghĩa là lần lượt nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
SW
1
Những câu hỏi liên quan
15 tháng 12 2021
Gọi chiều dài , chiều rộng của hình chữ nhật đó lần lượt là a ,b (cm) ; (a ,b >0 ) Có chiều dài , chiều rộng của hình chữ nhật đó tỉ lệ với 5 ; 3 => \(\frac{a}{5}\)= \(\frac{b}{3}\) Vì 2 lần chiều dài hơn 3 lần chiều rộng nên : 2a - 3b = 8 Có \(\frac{a}{5}\)=\(\frac{b}{3}\) => \(\frac{2a}{10}\)= \(\frac{3b}{9}\) Áp dụng tính chất của dãy tỉ số bằng nhau , ta có \(\frac{2a}{10}\) = \(\frac{3b}{9}\) = \(\frac{2a-3b}{10-9}\) = \(\frac{8}{1}\) = 8 Có \(\frac{a}{5}\) = 8 => 8.5=40 \(\frac{b}{3}\) = 8 = > 8.3=24 Chu vi hình chữ nhật đó là : ( 40+ 24) .2 =128 ( cm ) Vậy chu vi hình chữ nhật đó là 128 cm
17 tháng 4 2022
Tổng số phần bằng nhau là :
3 + 1 = 4 ( phần )
Đường chéo ngắn là :
104 : 4 x 1 = 26 ( cm )
Đường chéo dài là :
104 - 26 = 78 ( cm )
Vậy diện tích hình thoi là \(\dfrac{26\times78}{2}=1014(cm2)\)
8 tháng 8 2021
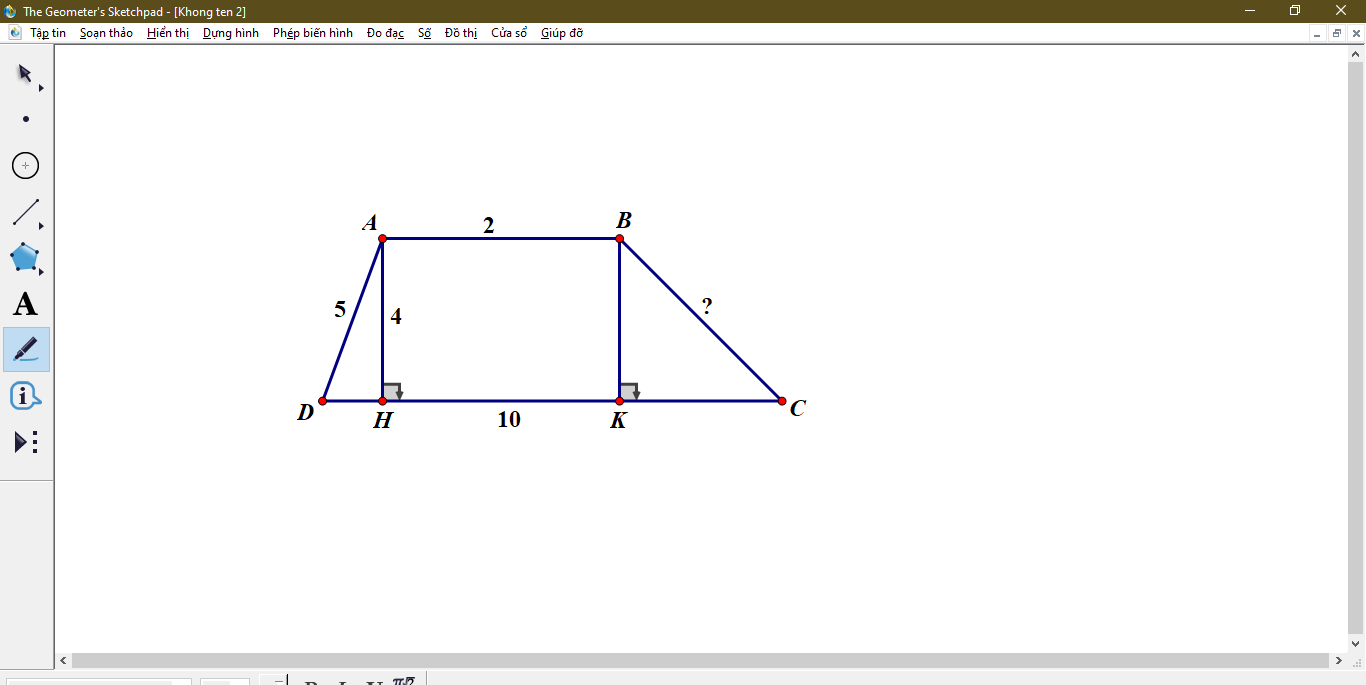
Xét \(\Delta ADH\) có \(AH^2+DH^2=AD^2\)
\(\Rightarrow DH^2=5^2-4^2=9\Rightarrow DH=3\)
Ta có ABKH là hcn
\(\Rightarrow\left\{{}\begin{matrix}AB=HK=2\\AH=BK=4\end{matrix}\right.\)
Ta có \(DH+HK+KC=DC\)
hay \(3+2+KC=10\Rightarrow KC=5\)
Xét \(\Delta BKC\), theo định lí Pytago có: \(BC=\sqrt{BK^2+KC^2}=\sqrt{5^2+4^2}=\sqrt{41}\left(cm\right)\)
TP
1
18 tháng 11 2017
=> a+1 chia hết cho 2;3;4;9
=> a+1 là BC của 2;3;4;9
Mà a nhỏ nhất => a+1 nhỏ nhất => a+1 là BCNN của 2;3;4;9
=> a+1 = 36 => a = 35
Vậy a=35
k mk nha
29 tháng 12 2015
Bạn ra đề như hình vẽ mà, tụi mình đâu có biết hình như thế nào mà vẽ đây!
14 tháng 8 2023
Diện tích HCN :
\(20x15=300\)
Diện tích hình thoi :
\(\dfrac{1}{2}x25x16=200\)
Tỉ số diện tích hình thoi và HCN :
\(\dfrac{300}{200}=\dfrac{3}{2}\)
NN
15 tháng 8 2018
Trong hình thang ABCD có: AE=ED(...)
BF=FC(...)
suy ra EF là đường trung bình của hình thang ABCD
suy ra EF//AB//DC suy ra EF//CD (1)
Trong tam giác ADC có: AE=ED(..)
AM=MC(...)
suy ra EM là đường trung bình của tam giác ADC
suy ra EM//CD (2)
Trong tam giác BDC co BN=ND(...)
BF=FC(...)
suy ra FN là đường trung bình của tam giác BDC
suy ra NF//CD(3)
Từ (1);(2) và (3) suy ra
E;N;M;E thẳng hàng
Vì EM là đường trung bình của tam giác ADC (cmt) nên \(EM=\frac{1}{2}CD\)
Trong tam giác ABD có: AE=DE(...)
DN=BN(....)
do đó EN là đường trung bình của tam giác ABD
\(\Rightarrow EN=\frac{1}{2}AB\)
Ta có NE+MN=EM
\(\Rightarrow MN=EM-NE=\frac{1}{2}CD-\frac{1}{2}AB=\frac{1}{2}\left(CD-AB\right)\)
help me please!